a) \(cos\alpha=m/(2R).\)
c) \(\alpha=37.76^0\)
d) \(\angle OEG = 115.38^0\)
1. Дана окружность с центром в точке \(O\) и радиусом \(R.\) Точка \(A\) лежит вне окружности, прямая \(AD\) касается окружности в точке \(D\), прямая \(AB\) пересекает окружност в двух точках \(C\) и \(B\), причем точка \(B\) лежит на отрезке \(AC.\) Дано, что \(\angle AOD = \alpha,\) и \(\angle AOB=\beta.\)
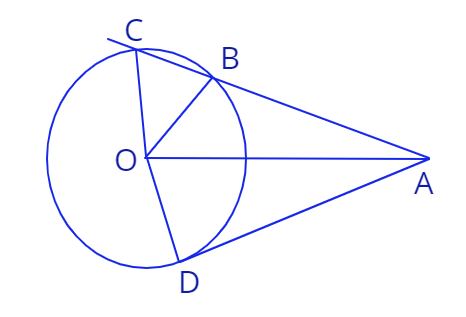
а) Найдите длину отрезка \(AO.\)
в) Найдите длину отрезка \(AB.\)
с) Дано, что \(|AB|=\sqrt{2}R\), докажите, что \(cos\beta = \frac{sin^2\alpha}{2cos\alpha}\)
d) Докажите, используя условие пункта c), что радиус окружности, описанной вокруг треугольника \(\triangle ADO\) равен \(\frac{5}{2\sqrt7}R\) и найдите величины углов \(\alpha\) и \(\beta.\)
2. Четырехугольник \(ABCD\) вписан в окружность с центром в точке \(O\) и радиусом \(R\). Угол \(\angle DAB\) острый и равен \(\alpha.\)
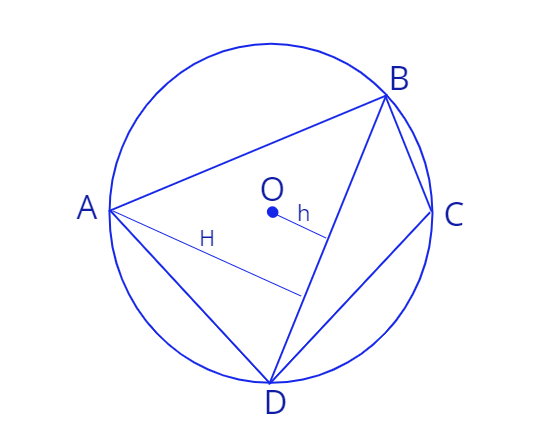
а) Найдите длину диагонали \(BD.\)
в) Вычислите \(\alpha\) , если \(|BC|=R, |CD| = R\sqrt2\)
с) \(BD\) - биссектриса угла \(\angle ABC\). Вычислите величину угла \(\angle ABD.\)
d) Найдите отношение высот треугольников \(\triangle ABD\) и \(\triangle BOD,\) опущенных на сторону \(BD.\)
3. Дана окружность с центром в точке \(O\) и радиусом \(R.\) Точка \(E\) лежит вне окружности, прямая \(ED\) касается окружности в точке \(D\), прямая \(EO\) пересекает окружность в двух точках \(A\) и \(B\), причем точка \(A\) лежит на отрезке \(EO.\) Хорда \(CD\) пересекает \(AB\) в точке \(F,\) \(\angle ADE = \alpha\)
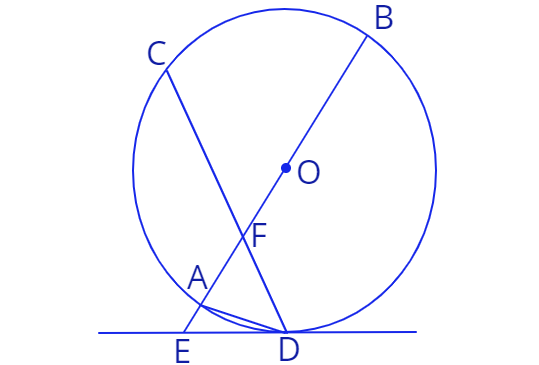
а) Найдите \(\angle BAD.\)
в) Дано, что \(|ED|=|FD|\), найдите \(\angle CDA.\)
с) Найдите площадь треугольника \(\triangle AFD.\)
d) Чему равно отношение площадей \(\frac{S_{AFD}}{S_{AED}}?\)
e) Дано, что \(\frac{S_{AFD}}{S_{AED}} = 1+\sqrt3,\) найдите \(\alpha.\)
4. Треугольник \(\triangle ABC\) тупоугольный, угол \(\angle BAC > 90^0.\) Дано, что \(|AB|+|AC| = 4a, \:|AB|:|AC|=3:5,\) площадь треугольника \(\triangle ABC\) равна \(\frac{15\sqrt3}{16}a^2, \: a-\) параметр.
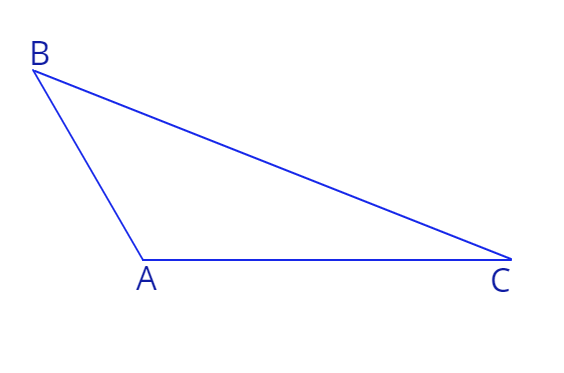
а) Вычислите величину угла \(\angle BAC\)
в) Вычислитк углы \(\angle ABC\) \(\angle ACB\)
с) В окружность, описанную вокруг треугольника\(\triangle ABC,\) можно вписать правильный пятиугольник, площадь которого равна \(100.\) Вычислите \(\alpha.\)
5. Дан треугольник \(\triangle ABC,\) точка \(D\) лежит на стороне \(AB,\) точка \(F\) на стороне \(BC,\) \(DF || AC,\) точки \(G\) и \(N\) лежат на стороне \(AC,\) четырехугольник \(DFNG\) является равнобедренной трапецией, \(|GN|<|DF|,\) \(\angle BAC = \alpha, \:\angle FNC = \beta, |AD|=7, \:|FC|=4,\:\angle FCN = 2\alpha\)
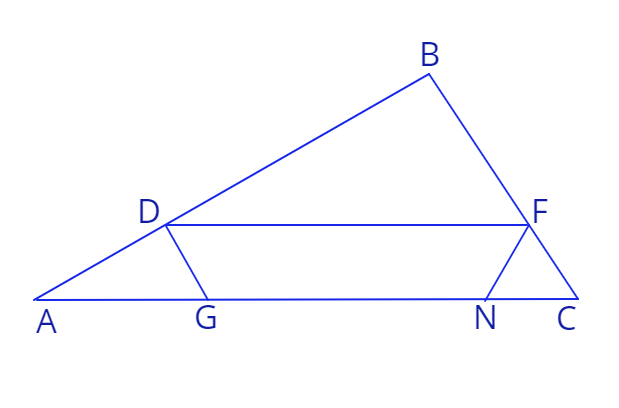
а) Докажите, что \(\frac{|FN|}{sin\alpha} = \frac{|AD|}{sin\beta}\)
в) Вычислите \(\alpha.\)
с) Площадь треугольника \(\triangle BDF\) равна \(56.\) Найдите длину \(|DF|.\)
d) Чему равно отношение радиусов окружностей, описанных вокруг треугольников \(\triangle FNC\) и \(\triangle DAG?\)
6. Треугольник \(\triangle BCD\) вписан в окружность с центром в точке \(O\) и радиусом \(R\). Точки \(O, E\) лежат на стороне \(BD,\:OE=ED.\) (см. рисунок)
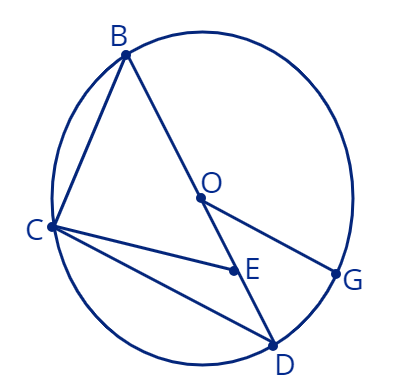
Обозначим \(CD=m,\:\angle CDB = \alpha\).
а) Выразите \(cos\alpha\) используя \(R\) и \(m\).
в) Докажите, что \(CE=(1/2)\sqrt{2m^2+r^2}\).
Дано, что \(BC=EC\).
с) Вычислите \(\:\alpha\).
Радиус \(OG\) параллелен стороне \(CD\).
d) Вычислите величину угла \(\angle OEG\).
a) \(cos\alpha=m/(2R).\)
c) \(\alpha=37.76^0\)
d) \(\angle OEG = 115.38^0\)
7. Дальтон \(ABCD\) вписан в окружность радиуса \(R.\:\) Хорда \(AC\) - большая диагональ дальтона. Точка \(O\) - центр окружности, вписанной в треугольник \(\triangle ABC\)(см. рисунок).
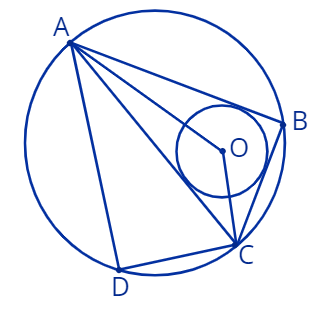
Обозначим \(\angle CAB=\alpha\)
а) Найдите углы треугольника \(\triangle AOC\) , выразив их через \(\alpha.\)
в) Выразите длину отрезка \(AO\) через \(R\) и \(\alpha.\)
Дано, что длина отрезка \(AO\) равна \(R\sqrt2\)
с) Найдите величину угла \(\alpha\).
Дано, что площадь дальтона равна \(16\sqrt3.\)
d) Найдите \(R.\)
e) Найдите расстояние между центром окружности, в которую вписан дальтон, и центром окружности, вписанной в треугольник \(\triangle ABC.\)
a) \(135^0,\:\alpha/2,\:45^0-\alpha/2.\)
b) \(AO=2R(cos (\alpha /2)-sin (\alpha /2)).\)
C) \(\alpha =30^0.\)
d) \(R=4.\)
e) \(4\sqrt{2-\sqrt3}.\)
8. Около треугольника \(ABC\) описана окружность с радиусом \(R\). Касательная к окружности, проходящая через точку \(B\) пересекается со стороной \(AC\) в точке \(D\) (см. рисунок). Обозначим \(\angle ABD=\alpha\). Дано, что \(\angle DBC=120^0\).
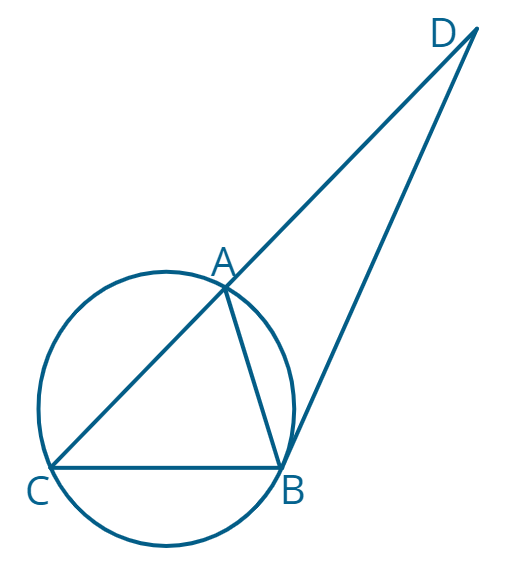
а) Найдите длины сторон \(AB\) и \(BC\), используя \(\alpha\) и \(R\).
Известно, что отношение площади треугольника \(\triangle BDC\) к площади треугольника \(\triangle BDA\) равно \(1.8.\)
в) Найдите \(\alpha\).
Дано, что радиус окружности, вписанной в треугольник \(\triangle BDA\) равен \(6.\)
с) Найдите \(R.\)
a) \(AB=2R\cdot sin(\alpha),\:\:BC=\sqrt3R,\)
b) \(sin(\alpha)=\sqrt{15}/6\),
c) \(R=6(\sqrt5+\sqrt{21}+6)/5.\)
9. Дана трапеция \(ABCD\: (AB\:||\:DC)\), вписанная в окружность. Продолжения сторон \(AD\) и \(BC\) пересекаются в точке \(E\).
Обозначим \(AC=k,\:\angle CDE=\alpha\). Дано: \(\angle ACB =60^0\).
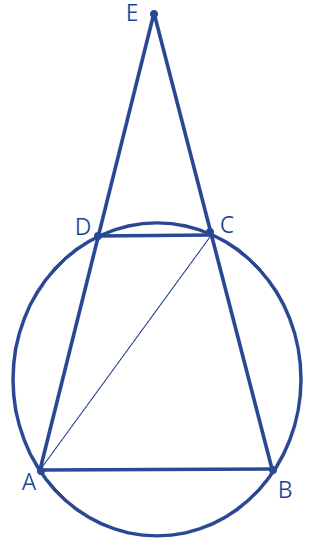
а) Найдите углы треугольника \(\triangle ACE\)
в) Выразите при помощи \(\alpha\) и \(k\) длины сторн \(AB\) и \(DC\).
Известно, что площадь треугольника \(\triangle ABE\) в \(3\) раза больше площади треугольника \(\triangle DCE.\)
с) Найдите величину угла \(\alpha.\)
d) Найдите значение \(k\), при котором длина медианы к стороне \(EC\) в треугольнике \(\triangle AEC\) равна \(\sqrt7.\)
a) \(\angle AEC=180^0-2\alpha, \:\angle EAC=2\alpha-120^0,\:\angle ECA=120^0.\)
b) \(|AB|=(k\sqrt3)/2sin\alpha,\:|DC|=(k\cdot sin(2\alpha-120^0))/sin\alpha,\)
c) \(\alpha=75^0,\)
d) \(k=2.\)