БАГРУТ

1. Дана функция \(f(x)=x^3+4x^2.\)

а) Напишите уравнение касательной к графику функции \(f(x)\) в точке \(B(t,f(t)).\)

в) Какова область значений \(t,\) если известно, что \(t < 0\) и касательная к графику функции пересекает ось \(y\) в точке \(C\) в области отрицательных значений.

с) Найдите максимальную площадь треугольника \(BOC, \:O-\) точка начала координат.

2. Даны две функции \(f(x)=x^3\:\) и \(\:g(x)=\sqrt{f(x)}.\)

а) Найдите области определения функций.

в) Найдите координаты точек пересечения графиков функций \(f(x)\) и \(g(x).\)

с) Дано, что отрезок \(AB\) параллелен оси \(x,\) точка \(A\) лежит на графике функции \(f(x)\) между точками пересечения графиков функций \(f(x)\) и \(g(x).\) Точка \(B\) лежит на графике функции \(g(x).\) Чему равна длина отрезка \(AB,\) если координата точки \(A\) по оси \(x\) равна \(t?\)

d) Найдите максимальную площадь треугольника \(ABO, \:O-\) точка начала координат.

e) Найдите максимальную длину отрезка \(AB\) и площадь треугольника \(ABO,\) когда длина отрезка \(AB\) максимальна.

3. На координатной плоскости задана точка \(C(a,b).\) Через точку \(C\) проводят прямую под углом \(\alpha\) к оси \(x\) , пересекающую оси координат в точках \(A\) и \(B\)

а) Чему равна длина отрезка \(AB?\)

в) Известно, что \(a=2b,\) найдите \(\alpha,\) для которого длина отрезка \(AB\) минимальна.

с) Чему равно \(b,\) если \(a=2b\) и минимальная длина отрезка \(AB\) равна \(8.\)

4. Дана функция \(f(x)=\frac{4}{\sqrt x}\) в области \(x>0.\) Точка \(A\) лежит на графике функции \(f(x).\)

а) Найдите длину отрезка \(AO,\:O-\) точка начала координат.

в) Чему равна минимальная длина отрезка \(AO?\)

с) Чему равен угол между касательной к графику функции в точке \(A\) и отрезком \(AO,\) когда длина отрезка \(AO\) минимальна?

d) Для \(x\in[{-4},{-1}]\) задана функция \(g(x)=-f(-x).\) Найдите координаты точки, расположенной на графике функции \(g(x),\) расстояние от которой до начала координат минимально.

e) Найдите координаты точки, расположенной на графике функции \(g(x),\) расстояние от которой до начала координат максимально.

5. Дана функция \(f(x)=-x^2+1.\) В точке \(B(t,f(t)),\: t > 0, \) лежащей на графике функции, провели касательную к графику функции.

а) Найдите уравнение касательной.

в) При каком значени \(t\) площадь \(S\) фигуры, заключенной между графиком функции \(f(x)\), касательной к функции, проведенной в точке \(B\) и осями координат будет минимальной?

с) Чему равно отношение площади \(S\) к площади фигуры заключенной между графиком функции \(f(x)\) и осями координат?

d) При каком \(t\) это отношение минимально,

e) При каком \(t\) это отношение максимально?

6. Дан ромб \(ABCD\). Точка \(E\) — середина стороны \(BC\). Обозначим \(\angle ECD = x\). Дано, что площадь треугольника \(\triangle ECD\) равна 25.

а) Выразите длину стороны ромба через \(x.\)

в) Вычислите минимальную длину отрезка \(DE.\)

7. Дана окружность с диаметром \(AB.\) Радиус окружности равен \(10.\) Точка \(P\) располагается на диаметре \(AB\) между центром окружности и точкой \(B.\) Через точку \(P\) проводят перпендикуляр к \(AB\) , пересекающий окружность в точках \(C\) и \(D.\) Найдите максимальную площадь треугольника \(ACD.\)

8. Даны функции \(f(x)=\sqrt{-x^2+7x},\:\:g(x)=\sqrt{14-2x}.\)

а) Найдите области определения функций.

в) Найдите координаты точек пересечения графиков функций \(f(x)\) и \(g(x).\)

Фигура заключенная между графиками функций \(f(x)\), \(g(x)\), прямыми \(x=a,\:\:x=a+1\) и осью \(x\) вращается вокруг оси \(x\), где \(a\) - параметр и \(a\in [1,2].\)

c) Найдите значение параметра \(a\), для которого объем полученного тела вращения максимален.

d) Найдите значение параметра \(a\), для которого объем полученного тела вращения минимален.

9. Прямая с угловым коэффициентом \(k=-2\) пересекает ось \(x\) в ее положительной части в точке \(B\) и ось \(y\) в ее положительной части в точке \(A\). Точка \(D\) лежит на прямой \(AB\) в первой четверти координатной плоскости (см. рисунок). Точка \(E\) лежит на оси \(x\) так, что отрезок \([DE]\) параллелен оси \(y\). Обозначим длину отрезка \(OE\) через \(p.\)

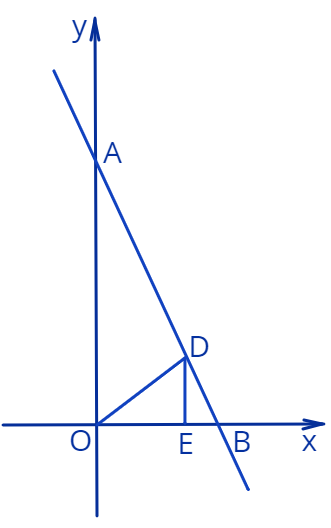
Дано: площадь треугольника \(\triangle OED\) равна \(p/2.\)

а) Напишите уравнение прямой \(AB\) используя \(p\).

в) Найдите значение \(p\) при котором отношение площади треугольника \(\triangle OED\) к площади треугольника \(\triangle ABO\) максимально.

Ответ

10. Точка \(E\) - это середина отрезка \(AB\). На отрезке \(AB\) построили прямоугольник \(ABCD\) и прямоугольный треугольник \(\triangle AFB,\:\:\angle AFB=90^0,\) как показано на рисунке.

Дано: \(\angle ECB=x,\:\:\angle FAB=2x.\)

Обозначим длину отрезка \(AB\) через \(h\).

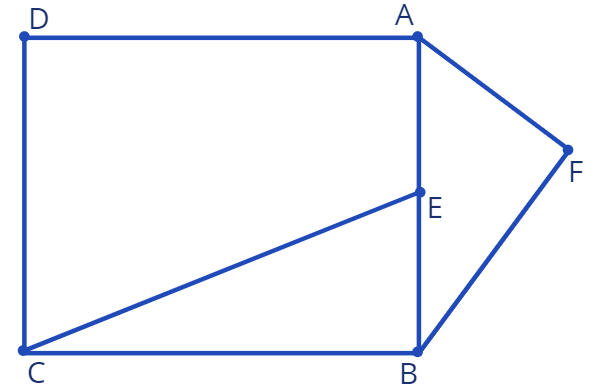
а) Найдите возможную область значений \(x\).

в) Выразите через \(x\) и \(h\) разность длин отрезков \(|CE|-|AF|\).

c) Найдите значение \(x\), при котором разность длин отрезков из пункта b) будет минимальной.

d) Для значения \(x\), найденного в пункте c), найдите отношение площади прямоугольника \(S_{ABCD}\) к площади треугольника \(S_{AFB}\).

Ответ





‹ ›