a) \(-x^2+4x+5=0\:=>x_{1,2}=-1;\:5\:=>A(-1,0),\:B(5,0)\)
b) \(x_c=(-4)/(-2)=2\:=>C(2,9)\)
c) \(x\in(-\infty,2)\) функция возрастает, \(x\in(2,+\infty)\) функция убывает.
d) \(S_{ACO}=(1/2)|AO|\cdot y_c=(1/2)\cdot1\cdot9=4.5\)
1. Дана функция \(y= -x^2+4x+5\)
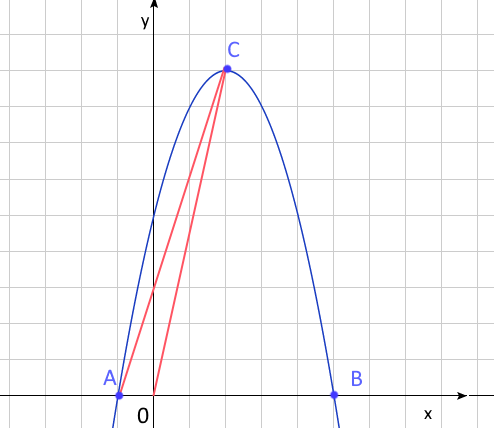
a) Найдите координаты точек \(A\) и \(B\) - точек пересечения графика функции с осью \(x\).
b) Найдите координаты точки \(C\) - вершины параболы.
c) Найдите области убывания и возрастания функции.
d) Найдите площадь треугольника \(\triangle ACO\) , где \(O\) - точка начала координат.
2. Дана функция \(y= x^2-6x-7\)
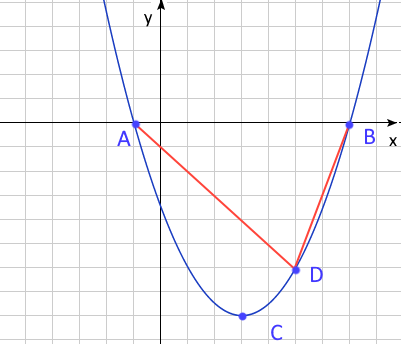
a) Найдите координаты точек \(A\) и \(B\) - точек пересечения графика функции с осью \(x\).
b) Найдите координаты точки \(C\) - вершины параболы.
c) Найдите области убывания и возрастания функции.
d) Координата точки \(D\) по оси \(x\) равна 5. Найдите площадь треугольника \(\triangle ABD\).
a) \(x^2-6x+78=0\:=>x_{1,2}=-1,7\:=>A(-1,0),\:B(7,0)\)
b) \(x_c=6/(2)=3\:=>C(3,-16)\)
c) \(x\in(-\infty,3)\) функция убывает, \(x\in(3,+\infty)\) функция возрастает.
d) \(D(5,-12)\:=>S_{ABD}=(1/2)|AB|\cdot |y_D|=(1/2)\cdot8\cdot12=48\)
3. Дана функция \(y= -x^2+2x+8\)
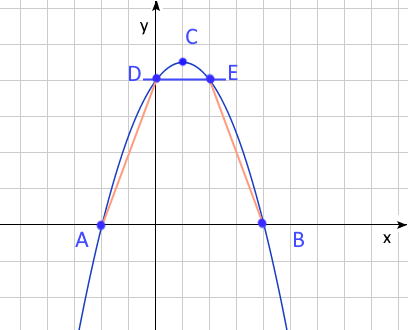
a) Найдите координаты точек \(A\) и \(B\) - точек пересечения графика функции с осью \(x\).
b) Найдите координаты точки \(C\) - вершины параболы.
c) Найдите области убывания и возрастания функции.
d) Найдите координаты точки \(D\) - точки пересечения графика функции с осью \(y\).
e) Прямая \(DE\) параллельна оси \(x\). Точка \(E\) лежит на графике функции. Найдите площадь трапеции \(ADEB\).
a) \(-x^2+2x+8=0\:=>x_{1,2}=-2,4\:=>A(-2,0),\:B(4,0)\)
b) \(x_c=-2/(-2)=1\:=>C(1,9)\)
c) \(x\in(-\infty,1)\) функция возрастает, \(x\in(1,+\infty)\) функция убывает.
d) \(x=0\:=>y=8\:=>D(0,8)\:=>E(2,8)\)
e) \(S_{ADES}=(1/2)(|AB|+|DE|)\cdot{y_D}=(1/2)(6+2)\cdot8=32\)
4. Дана функция \(y= -x^2+2x+15\)
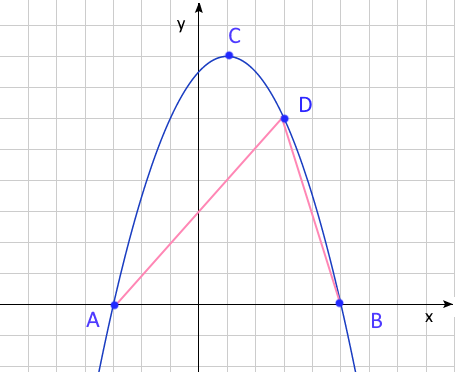
a) Найдите координаты точек \(A\) и \(B\) - точек пересечения графика функции с осью \(x\).
b) Найдите координаты точки \(C\) - вершины параболы.
c) Найдите области убывания и возрастания функции.
d) Координата точки \(D\) по оси \(x\) равна \(3\). Найдите координаты точки \(D\).
e) Найдите площадь треугольника \(\triangle ABD\)
a) \(-x^2+2x+15=0\:=>x_{1,2}=-3,5\:=>A(-3,0),\:B(5,0)\)
b) \(x_c=-2/(-2)=1\:=>C(1,16)\)
c) \(x\in(-\infty,1)\) функция возрастает, \(x\in(1,+\infty)\) функция убывает.
d) \(D(3,12)\)
e) \(S_{ABD}=(1/2)|AB|\cdot y_D=(1/2)\cdot8\cdot12=48\)
5. Дана функция \(y= -x^2-2x+8\)
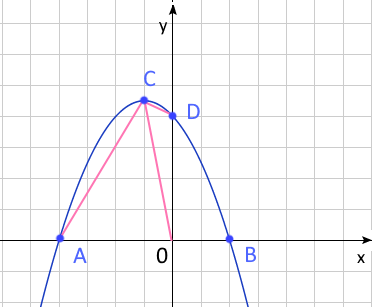
a) Найдите координаты точек \(A\) и \(B\) - точек пересечения графика функции с осью \(x\).
b) Найдите координаты точки \(C\) - вершины параболы и точки \(D\) - точки пересечения графика функции с осью \(y\).
c) Найдите области убывания и возрастания функции.
d) Найдите области отрицательных значений данной функции.
e) Найдите площадь треугольника \(\triangle OCA\), где \(O\) - точка начала координат.
f) Найдите площадь треугольника \(\triangle OCD\)
a) \(-x^2-2x+8=0\:=>x_{1,2}=-4,2\;=>A(-4,0),\:B(2,0)\)
b) \(x_c=2/(-2)=-1\;=>C(-1,9),\:x_D=0\:=>D(0,8)\)
c) \(x\in(-\infty,-1)\) функция возрастает, \(x\in(-1,+\infty)\) функция убывает.
d) На интервале \(x\in(-\infty,-4)\cup(2,+\infty)\) значения функции отрицательны.
e) \(S_{OCA}=(1/2)|AO|\cdot y_c=(1/2)\cdot 4\cdot 9=18\)
f) \(S_{OCD}=(1/2)|OD|\cdot|x_c|=(1/2)\cdot 8\cdot1=4\)
‹ ›