1. Дана функция \(f(x) = \frac{x^2-9}{\sqrt{x+a}}, \: a - \) положительный параметр.
а) Найдите область определения.
в) Известно, что у функции нет асимптот, перпендикулярных осям координат. Найдите \(a.\)
с) Найдите координаты точек пересечения графика функции с осями.
d) Найдите координаты точек экстремума и определите их тип, найдите области возрастания и убывания функции.
e) Начертите схематический график функции.
f) Даны функции \(g(x) = -f(x+2), h(x)=|f(x)|.\) Найдите области определения функций \(g(x), f(x).\)
g) Найдите координаты точек максимума функций \(g(x), f(x).\)
h) Известно, что \(\int_{-1}^{3}h(x)dx = \int_{-3}^{k}g(x)dx, \:k>-3.\) Найдите \(k.\)
2. Дана функция \(f(x) = 2x + \frac{2}{x}\)
а) Найдите область определения функции.
в) Определите четность функции.
с) Найдите области возрастания и убывания функции.
d) Дана функция \(g(x)=f(x)\cdot f'(x),\) определенная в той же области, что и \(f(x),\; f'(x)\) - производная функции \(f(x).\)
е) Найдите координаты точек пересечения графика функции \(g(x)\) с осью \(x.\)
f) Начертите схематические графики функций \(f(x), f'(x), g(x).\)
g) Вычислите площадь фигуры, заключенной между осью \(x,\) графиком функции \(g(x)\) и прямыми \(x=1/4,\: x=4.\)
h) Чему равен интеграл \(\int_a^{\frac{1}{a}}g(x)dx, \: 0 < a < 1 ?\)
i) Дана функция \(h(x) = \int_1^xf'(t)dt,\) определенная для \(x\geq{1}.\) Найдите координаты точки экстремума \(h(x)\) и определите ее тип.
3. Дана функция \(f(x)=\frac{x^2}{(x^3-m)^2} ,\:m -\) положительный параметр.
а) Найдите область определения функции.
в) Найдите координаты точек экстремума и определить их тип.
с) Найдите уравнения асимптот функции, перпендикулярных осям координат.
d) Найдите значение \(m,\) если известно, что у функции есть экстремум в точке с координатой \(x=-1\)
e) Начертите схематический график функции.
f) Начертите схематический график функции \(g(x)=k\cdot f(x),\: k - \) отрицательный параметр.
g) Через левую точку экстремума функции \(g(x)\) проводят прямую, перпендикулярную оси \(x.\) Найдите площадь фигуры, ограниченной этим перпендикуляром, осью \(x\) и графиком функции \(g(x).\)
4. Дана функция \(f(x)=6x(x^3-1)^3\)
а) Найдите координаты точек пересечения графика функции с осями.
в) Найти координаты точек экстремума и определить их тип, найдите области возрастания и убывания функции.
с) Начертите схематический график функции.
d) При каких значениях \(k\) прямая \(y=k\) является касательной к графику функции.
e) При каких значениях \(k\) прямая \(y=k\) пересекает график функции только в двух точках, расположеных справа от оси \(y.\)
f) При каких значениях \(k\) прямая \(y=k\) пересекает график функции только в двух точках, расположеных по обе стороны от оси \(y.\)
g) При каком \(a\) интеграл \(\int_0^af(x)dx\) принимает минимальное значение
5. Дана функция \(f(x)=\frac{3x}{4x^2-1}\)
а) Найдите область определения функции.
b) Найдите области возрастания и убывания функции и области отрицательных и положительных значений функции.
с) Найдите область определения функции \(g(x)=\sqrt{f(x)}\)
d) Найдите уравнения асимптот, перпендикулярных осям для функции \(g(x).\)
e) Начертите схематический график функции \(g(x),\) если известно, что у функции есть единственная точка перегиба с координатой \(x\) меньше нуля.
f) Начертите схематический график \(g '(x) \)- производной функции.
g) Найдите область определения функции \(h(x) = \frac{\sqrt{3x}}{\sqrt{4x^2-1}}.\)
6. Дана функция \(f(x)=3x + 2\sqrt{x^2-2x}\)
а) Найдите область определения функции.
inline-block) Найдите область определения \(f'(x)\) производной функции \(f(x).\)
с) Найдите уравнения асимптот, перпендикулярных осям координат, для функции \(f'(x).\)
d) Найдите координаты точек пересечения с осью \(x\) графика функции \(f'(x).\)
e) Начертите схематический график функции \(f'(x),\) если известно, что у функции \(f'(x),\) нет точек экстремума.
f) Найдите координаты точек экстремума функции \(f(x)\) и определите их тип.
g) Начертите схематический график функции \(f(x).\)
h) Может ли прямая \(y=4x+c, \:c -\) параметр, являться касательной к графику функции \(f(x)?\)
7. Дана функция \(f(x)=x^n\cdot (x+1)^2, n > 1, n\) - натуральное. Функция \(f(x)\) определена для любого \(x.\)
а) Найдите координаты точек пересечения графика функции с осями координат.
b) Найдите области положительных и отрицательных значений данной функции.
с) Найдите координаты точек экстремума функции \(f(x)\) и определите их тип.
d) Начертите схематические графики функции \(f(x)\) для четных и нечетных \(n.\)
e) Дана функция \(g(x)=a\cdot f(x-2)\:, \:a-\) положительный параметр. Обозначим через \(S\) площадь фигуры, заключенной между графиком функции \(g(x)\) и осью \(x\). Выразите через \(S\) площадь фигуры, заключенной между графиком функции \(f(x)\) и осью \(x\).
8. Дана функция \(f(x)=(2a-x^2)/x,\: x \neq 0, \:a\) - положительный параметр.
а) Найдите уравнения асимптот функции \(f(x)\), перпендикулярных осям координат.
b) Определите четность функции.
с) Найдите координаты точек пересечения графика функции с осями координат.
d) Найдите промежутки возрастания и убывания функции.
e) Найдите промежутки, на которых функция выпукла и на которых она вогнута.
f) Начертите схематический график функции \(f(x).\)
g) Дана функция \(g(x)= |f(x)|-b, \:b\) - положительный параметр. Область определения функции \(g(x)\) совпадает с областью определения функции \(f(x).\) Начертите схематический график функции \(g(x).\)
h) Известно, что точка \((3,-8)\) является точкой экстремума функции \(g(x).\) Найдите значение параметров \(a,\:b.\)
i) Дана функция \(s(x)= \int_{1}^{x} g(t)dt,\) которая определена для \(x>1.\)Определите тип точки экстремума функции \(s(x).\)
9. Дана функция \(f(x)=x+\sqrt{x^2-9}.\)
а) Найдите область определения функции \(f(x).\)
b) Найдите координаты точек пересечения графика функции с осью \(x.\)
с) Найдите промежутки возрастания и убывания функци \(f(x).\)
d) Найдите промежутки, на которых функция выпукла и на которых она вогнута.
e) Начертите схематический график функции \(f(x).\)
Дана функция \(h(x)=-f(-x),\) определенная в той же области, что и \(f(x).\)
f) Начертите схематический график функции \(h(x)\) на графике функции \(f(x).\)
Дано : \(a>5, \:a\) - параметр.
g) Сравните величины интегралов: \(S_1= \int_{a}^{a+1} (f(x)-h(x))dx,\:\:\:S_2= \int_{a+1}^{a+2} (f(x)-h(x))dx,\:\:\:S_3= \int_{1-a}^{2-a} (f(x)-h(x))dx.\)
10. Дана функция \(f(x)=(x^2-a^2)/(x-4)^2, 0 < a < 4\) - параметр.
а) Найдите область определения функции \(f(x).\)
b) Найдите уравнения асимптот функции \(f(x)\), перпендикулярных осям координат.
с) Найдите координаты точек пересечения графика функции с осями координат.
d) Найдите координату \(x\) точки экстремума функции \(f(x)\) и определите ее тип.
e) Начертите схематический график функции \(f(x).\)
Дана функция \(g(x)=x^2/(x-4)^2,\) определенная в той же области, что и \(f(x).\)
f) Докажите, что график функции \(g(x)\) полностью расположен над графиком функции \(f(x).\)
g) Выразите при помощи параметра \(a\) площадь фигуры, заключенной между графиками функций \(f(x)\) и \(g(x)\), прямой \(x=1\) и осью \(y\).
11. Дана функция \(f(x)=2x/\sqrt{x^2+x}\).
а) Найдите область определения функции \(f(x)\).
b) Пересекает ли график функции \(f(x)\) оси координат?
с) Найдите уравнения асимптот функции \(f(x)\), перпендикулярных осям координат.
d) Найдите промежутки возрастания и убывания функци \(f(x).\)
Известно, что у функции \(f(x)\) нет точек перегиба.e) Начертите схематический график функции \(f(x).\)
d) Пользуясь графиком функции \(f(x)\), определите какой из графиков на рисунке описывает вторую производную \(f''(x).\)
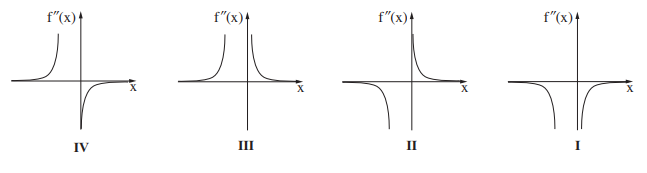
e) Вычислите площадь фигуры, заключенной между графиком второй производной \(f''(x)\), осью \(x,\) прямыми \(x=1\) и \(x=2.\).
‹ ›