БАГРУТ

1. В прямоугольнике \(ABCD\) точка \(H\) расположена на стороне \(AD.\) Отрезок \(CH\) пересекает диагональ \(BD\) в точке \(T.\) Четырехугольник \(ABTH\) может быть вписан в окружность. Известно, что \(|AH| = |HD|\)

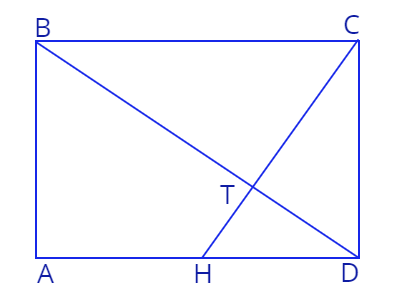
а) Докажите, что \(\triangle DAB \sim \triangle BTC\)

b) Вычислите отношение \(\frac {TH}{TC}\)

c) Найдите площади треугольников \(\triangle DTC\) и \(\triangle BTC,\) если дано, что площадь \(\triangle DTH\) равна \(S.\)

d) Найдите коэффициент подобия для треугольников \(\triangle DAB\) и \(\triangle BTC\)

e) Во сколько раз длина диагонали \(BD\) больше длины отрезка \(HD?\)

f) Чему равен радиус окружности, описанной вокруг четырехугольника \(ABTH,\) если \(DH = \sqrt3.\)

2. Дана окружность с центром в точке \(O\) и радиусом \(R.\) Точка \(A\) лежит вне окружности, прямая \(AB\) касается окружности в точке \(B\), прямая \(AO\) пересекает окружность в двух точках \(C\) и \(D\), причем точка \(C\) лежит на отрезке \(AO.\) Прямая \(AE\) перпендикулярна прямой \(AO\) и пересекает прямую \(BD\) в точке \(E.\)

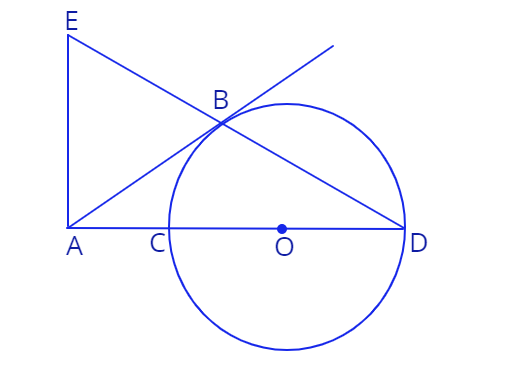
а) Чему равна углы треугольника \(\triangle ABE\), если угол \(\angle ADB = \alpha?\)

в) Докажите, что \(\frac{AB}{AC}=\frac{DB}{BC}.\)

с) Чему равен радиус окружности, если \(|DC|=2|AC|, |AE|=8.\)

d) Докажите, что \(\triangle ADE \sim \triangle DBC.\)

e) Во сколько раз площадь \(\triangle ADE\) больше площади треугольника \(\triangle DBC\), если выполняется условие пункта c)?

3. Дана окружность, отрезок \(\:BC\) - диаметр, радиус равен \(R,\) точка \(A\) лежит на окружности. Хорду \(CA\) продлили до точки \(G\), такой, что \(|CA| = |AG|.\) Отрезок \(GB\) пересекает окружность в точке \(D.\) Прямая \(CE\) является касательной к окружности в точке \(C\) и пересекает прямую \(BA\) в точке \(E.\) Известно, что \(\frac{S_{DBCA}}{S_{GAD}} = 15.\)

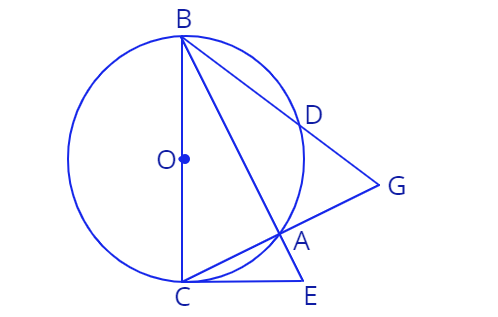
а) Докажиме, что прямая \(AB\) - биссектриса угла \(\angle DBC.\)

в) Докажите, что \(\triangle GBC \sim \triangle GAD.\)

с) Найдите отношение \(\frac{R}{AC}.\)

d) Найдите отношение площадей треугольников \(\triangle{CBE}\) и \(\triangle{ABC}.\)

4. Дана окружность с центром в точке \(O\) и радиусом \(R.\) Точка \(D\) лежит вне окружности, прямая \(AD\) касается окружности в точке \(A\), прямая \(DO\) пересекает окружност в двух точках \(B\) и \(E\), причем точка \(E\) лежит на отрезке \(DO,\) прямая \(BC\) параллельна прямой \(AD\) и пересекает окружность в точке \(C.\) \(AE - \) биссектриса угла \(\angle MAD,\) где \(M\) - точка тересечения прямых \(AC,\) и \(BD.\)

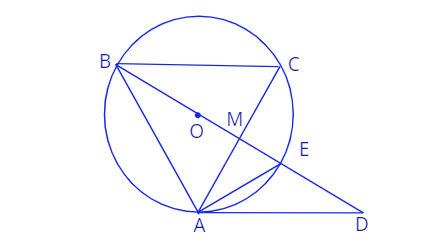
а) Докажиме, что \(|AB| = |AC|.\)

в) Докажите, что \(BM \perp AC.\)

с) Докажите, что \(|AE|=R.\)

d) Докажите, что \(ABCD\) - ромб.

5. \(AD\) и \(BE\) - биссектрисы углов в треугольнике \(\triangle ABC\), пересекающиеся в точке \(F.\) Известно, что \(\angle ACB = 60^0\)

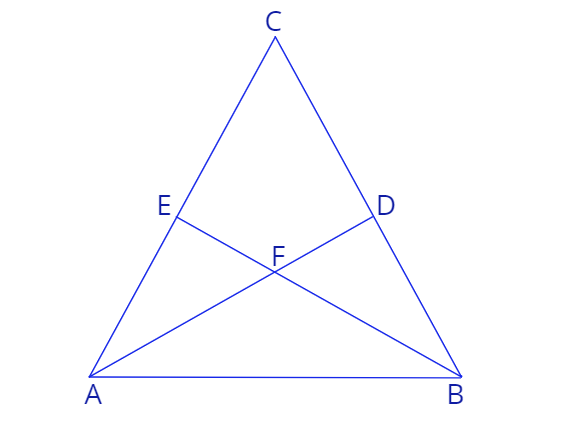
а) Докажиме, что четырехугольник \(DCEF\) можно вписать в окружность.

в) Известно, что \(FC\) - это диаметр окружности, описанной вокруг четырехугольника \(DCEF.\) Докажите, что треугольник \(\triangle ABC\) равносторонний.

с) Прямая \(CF\) пересекает сторону \(AB\) в точке \(G.\) Докажите, что длина \(|FG|\) равна радиусу окружности, описанной вокруг четырехугольника \(DCEF.\)

d) К окружности, описанной вокруг четырехугольника \(DCEF,\) проводят касательную в точке \(F\), которая пересекает стороны \(AC\) и \(BC\) в точках \(K\) и \(L.\) Найдите отношение \(\frac{KL}{AB}\)

6. Две окружности пересекаются в точках \(A\) и \(B\), отрезок \(CE\) проходит через точку \(B\) (см. рисунок).

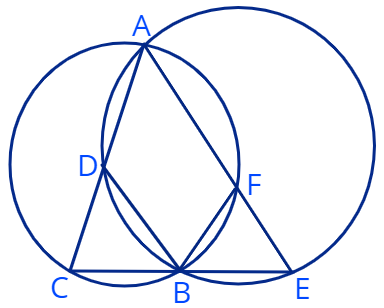
а) Докажите, что \(\triangle ACE \sim \triangle BCD.\)

Дано \(DC=FE\).

в) Докажите, что \( \triangle BFE = \triangle BCD\)

с) Докажите, что \(AC \cdot BE=AE \cdot BC\).

d) Докажите, что \(AB\) биссектриса угла \( \angle CAE\).

e) Докажите, что \(\angle DEC = \angle FCE\).

7. Точки \(A,\:B,\:C\:\) лежат на окружности. Точка \(E\) — это середина дуги \(BC\) (см. рисунок). В точке \(E\) проведена касательная к окружности. Касательная пересекает продолжение хорды \(AB\) в точке \(G\). Хорды ​\(AE\) и \(BC\) пересекаются в точке \(F\).

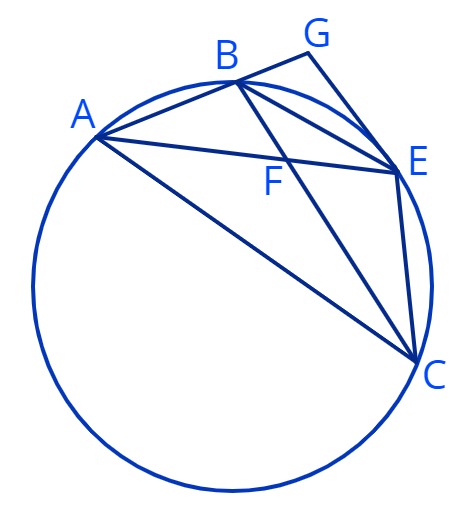
а) Докажите, что \( \triangle ACE = \triangle AEG\)

Дано \(AG=18,\:AE=9\sqrt6\).

в) Найдите длину хорды \(AC\).

с) Докажите, что \(BC // GE\).

Дано площадь треугольника \(\triangle ABF\) в 2 раза больше площади треугольника \(\triangle BEF\).

d) Найдите длину хорды \(AB\).

e) Найдите отношение площади треугольника \(\triangle ABF\) к площади треугольника \(\triangle AFC\).

Ответ

8. Дан прямоугольный треугольник \(\triangle ABC,\:\:\angle ACB = 90^0\). Окружность касается гипотенузы \(AB\) в точке \(F\), проходит через вершину прямого угла \(C\) и пересекает катеты \(AC,\:\:CB\) в точках \(G,\:\:H\) соответственно. Известно, что \(AB\:||\:GH\).

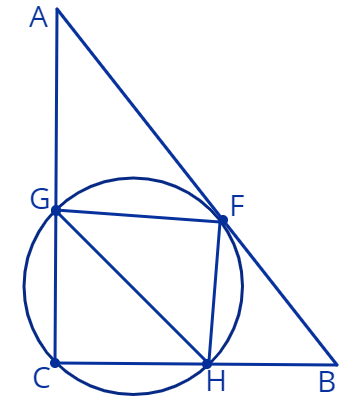
а) Доказать, что \(FG=FH\).

в) Найти величину угла \(\angle ACF.\)

с) Доказать, что \(\triangle GFC \sim \triangle FBC.\)

Диаметр окружности, содержащий точку \(F\), пересекает катет \(AC\) в точке \(E.\)

d) Доказать, что \(\angle FEB=\angle FCB\).

Ответ

9. Из точки \(B\), расположенной вне окружности, провели прямую, касательную к окружности в точке \(C\), и прямую, пересекающую окружность в точках \(E,\:A.\) Точка \(D\) лежит на окружности, и хорда \(CD\) параллельна хорде \(EA\). Хорды \(ED\) и \(AC\) пересекаются в точке \(K\).

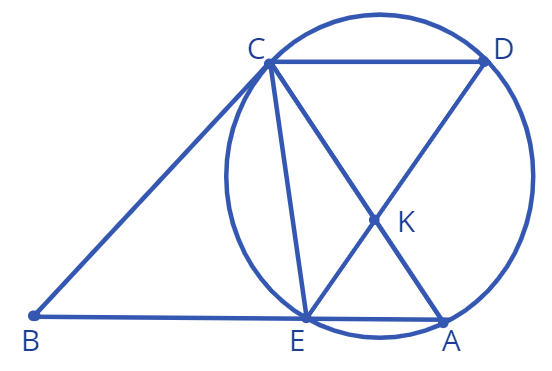
а) Докажите, что треугольники \(\triangle CEB\) и \(\triangle DCE\) подобны.

Дано: \(|AK|=3,\:\: |ED|=7.\) Площадь треугольника \(\triangle CEK =S.\)

в) Выразите площадь треугольника \(\triangle CKD\) через \(S.\)

Дано: \(|BC|=35/\sqrt{32}.\)

с) Выразите площадь треугольника \(\triangle CEB\) через \(S.\)

Точка \(O\) - центр данной окружности.

d) Докажите, что \(\angle COE = \angle CKE.\)

Дано: \(\angle CAE=45^0.\)

e) Объясните, почему через точки \(O,\:\:C,\:\:E,\:\:K\) можно провести окружность.

Ответ
‹ ›