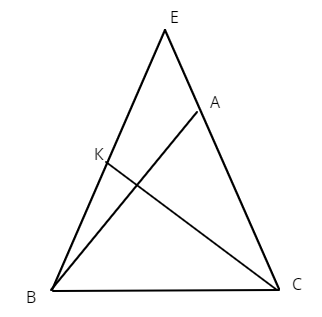
1. Дан треугольник \(\triangle ABC\), точка \(E\) лежит на \([BC]\) точка \(K\) лежит на продолжении \([AC]\) за точку \(A\) \(|AC| = 10, |AE| = 7, |CE| = 4, [AE] = [EB], [AC] = 4\cdot [KA]\)
а) Найти угол \(\angle AEC\)
в) Найти площадь \(\triangle ABC\)
с) \(S_{ABC} = 4\cdot S_{ABK}\), найти \(|KA|\)
d) Найти отношение \(S_{ABE}/ S_{AEC}\)
Решение
а) \(10^2 = 4^2 + 7^27 - 2\cdot 4\cdot 7 \cdot cos(\angle AEC)\)
\(\angle AEC = 128.68^0\)
в)\(S_{ABC} = (1/2)\cdot AE\cdot CE \cdot sin(\angle AEC) + (1/2)\cdot EB\cdot EA\cdot sin(\angle AEC) = 30\)
c) \(|KA| = (1/4)\cdot AC = 2.5\)
d) \(S_{ABE}/ S_{AEC} = BE/EC = 7/4 = 1.75\)
Ответ:\( а) 128.68^0 , в) 30 , c) 2.5 , d) 1.75\)
2. Дан остроугольный треугольник \(\triangle BEC, BE = EC\), точка \(A\) лежит на стороне \(EC, BE = 4\cdot AE\), угол \(\angle BAE\) равен \(120^0\). Точка \(K\) Лежит на стороне \(BE, BK = EK\). Площадь треугольника \(BEC\) равна \(18\).
а) Вычислите угол \(\angle EBA\)
в) Чему равна длина отрезка \(EA\)?
с) Чему равна длина отрезка \(CK\)?
Решение
а) \(BE/(sin\angle EAB) = EA/ (sin\angle EBA) =>\)
\(sin\angle EBA = (EA/EB)\cdot sin\angle EAB = 0.2165 => \angle EBA =12.5^0\)
в) \(\angle BEC = 180^0 - 120^0-12,5^0 = 47,5^0\)
\(S_{BEC} = (1/2)\cdot BE^2sin(47,5^0) = 18 => BE = 7 => EA = 1.75\)
с) По теореме косинусов \(CK^2=3.5^2+7^2 — 2\cdot 3.5\cdot 7\cdot cos(47.5^0) =28.146, CK = 5.3\)
Ответ: \(а) \angle EBA =12.5^0, в) EA = 1.75 , с) CK = 5.3\)
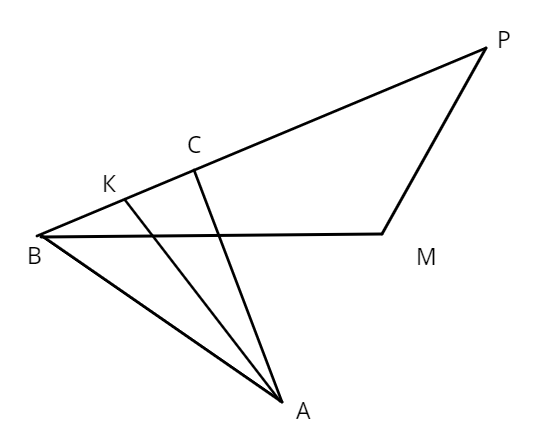
3. В треугольнике \(\triangle BPM\) угол \(\angle BMP\) тупой, точки \(C\) и \(K\) лежат на стороне \(BP, CP = 2\cdot BC, \angle BPM = 30^0, BM = 12\). В треугольнике \(BAC\) угол \(\angle BAC = 30^0, AK\) — биссектриса угла \(\angle BAC, AB = 10\), площадь \(\triangle ABC = 20.\)
а) Найдите длину \(AC\).
в) Найдите длину\( BC\).
с) Вычислите величину угла \(\angle BMP\).
d) Найдите углы треугольника \(\triangle ABK.\)
Решение
а)\( S_{ABC} = (1/2)\cdot AB\cdot AC\cdot sin(\angle BAC) => 20 = 0.5\cdot 10\cdot AC\cdot sin(30^0) => AC = 8\)
в) По теореме косинусов \(BC^2 =AB^2+AC^2-2\cdot AB\cdot AC\cdot cos(\angle BAC) => BC = 5\)
с) \(BP = 3\cdot BC\) (по условию). По теореме синусов \(BP/sin(\angle BMP)=BM/sin(\angle BPM)=>\)
\(sin(\angle BMP) = (15/12)\cdot sin(30^0) = 0.625 => \angle BMP = 141,32^0\) ( угол\(\angle BMP\) тупой по условию)
d) \(AB = 2\cdot BC\) и \(\angle BAC = 30^0\) (по условию) \(=>\angle BCA = 90^0 =>\angle KBA = 90^0-30^0 =60^0, \angle BAK = 15^0 =>\angle BKA = 180^0-60^0-15^0 = 105^0.\)
Ответ: \(а) AC = 8, в) BC = 5, с) \angle BMP = 141.32^0 , d)
\angle KBA = 60^0, \angle BAK = 15^0 , \angle BKA =105^0.\)
‹
›