1. Дана окружность \((y-6)^2 + (x-4)^2 = 25\) с центром в точке \(M\)
Эту окружность пересекает прямая \(y = x+1\) в точках \(A\) и \(B\)
а) Найдите координаты точек \(A\) и \(B\).
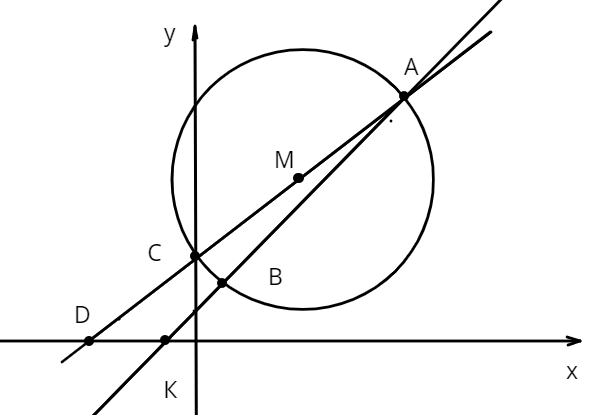
Прямая \(AM\) пересекает ось \(x\) в точке \(D\), а ось \(y\) в точке \(C\)
в) Найдите координаты точек \(C\) и \(D\)
с) Докажите, что прямая \(CB\) перпендикулярна \(AB\)
d) Напишите уравнение касательной к окружности в точке \(C\)
е) Вычислите площадь треугольника \(\triangle ABD\)
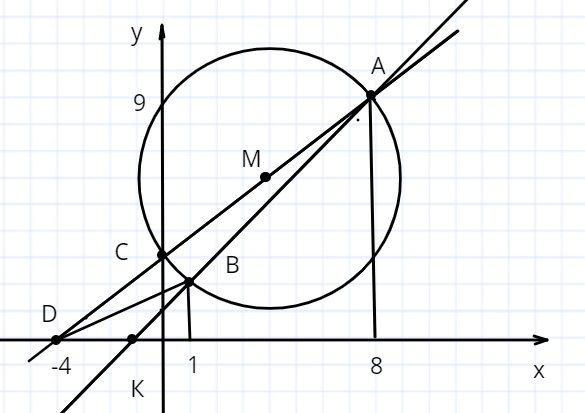
а) \(y = x+1\) прямая \(AB\)
\((x-5)^2 + (x-4)^2 = 25\)
\(2x^2 - 18x + 16 = 0\)
\(x_1 = 1, у_1 = 2, B(1,2)\)
\(x_2 = 8, y_2 = 9, A(8,9)\)
в) \(M(4,6)\), подставим координаты \(A\) и \(M\) в уравнение прямой \(y = mx +b\)
\(\begin{cases}9 = m\cdot 8 + b\\6 = m\cdot 4 + b\end{cases}\)
\(3 = 4\cdot m, \:m = 0.75, b = 3\)
уравнение прямой \(AM\): \( y = 0.75x + 3\)
точка с координатами \(C (0,3)\) лежит и на прямой , и на окружности.
Найдем координаты \(D: y = 0, 0 = 0.75x +3\), следовательно \(x = -4, D(-4,0)\)
с) Прямая \(AB\) : \(y = x+1\)
Прямая \(CB: C (0,3), B(1,2)=> y= -x + 3\)
\(1\cdot(-1) = -1\) следовательно прямые \(AB\) и\(CB\) перпендикулярны
d) Касательная к окружности в точке \(C\) перпендикулярна \(CM\) и пересекает ось \(y\) в точке \(3\)
\(AM\): \( y = 0.75x + 3\)
Уравнение касательной \(y = (-4/3)x + 3\)
е) Площадь треугольника \(\triangle ABD\) равна
\(S_{ABD}=(12\cdot 9)/2 - (5\cdot 2)/2 - 7\cdot 2 - (7\cdot7)/2 = 10.5\)
Ответ: \(а)\: A(8,9),\: B(1,2),\: в)\: C (0,3),\: D(-4,0), \:d)\: y = (-4/3)x + 3, \:е)\: 10.5\)
2. Точка\(A(1,8)\) лежит на окружности с центром в \(M(4,4).\)
а) Найдите уравнение окружности.
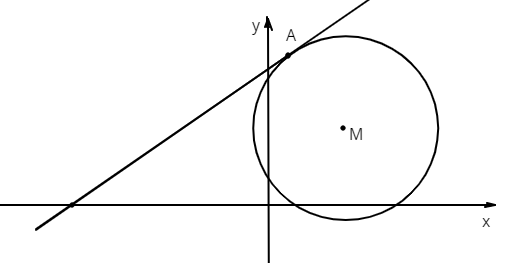
в) Найдите уравнение касательной к окружности, проходящей через точку\(A\)
На окружности лежит точка \(B\) с координатой \(0\) по оси \(y\) и координатой больше \(4\) по оси \(x\).
с) Найдите координаты точки \(B\).
d) Является ли \(AB\) диаметром?
На касательной лежит точка \(C\) с координатой \(2\) по оси \(y\). Точка \(D\) центр окружности, описанной вокруг треугольника \(\triangle ABC\).
е) Найдите площадь треугольника \(\triangle ADC\)
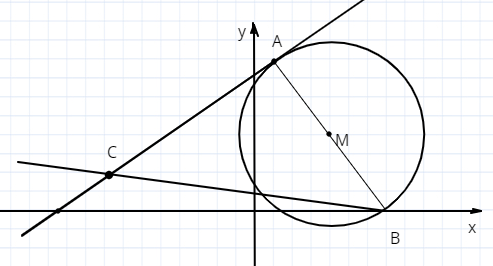
а)\( (1-4)^2 + (8 - 4)^2 = R^2 , R= 5,\)
\((х-4)^2 + (у-4)^2 =25\)
в) Прямая \(AM:\) \(\begin{cases}8 = m + b\\4 = 4\cdot m + b\end{cases}\)
\(m= - (4/3)\) и \(b = 28/3 \)
\(y = -(4/3)x + 28/3\)
Прямая, перпендикулярная к \(AM\) \(y = (3/4)x + b\) проходит через точку \(A => 8 = (3/4)\cdot1 + b,\:b = 29/4\).
Уравнение касательной \(\:4y = 3x + 29\)
с) \(B (7,0)\)
d) \(B\) лежит на прямой \(AM\), \(AB\) диаметр
е) \(C(-7,2)\), треугольник \(\triangle ABC\) прямоугольный, центр окружности, описанной вокруг \(\triangle ABC\) находится в центре отрезка \(CB.\)
\(|AB| = 10, |AC|^2 = (1 + 7)^2 + (8-2)^2 = 100, |AC| = 10\)
Площадь треугольника\(\:\triangle ADC\) равна половине площади треугольника \(\triangle ABC\)
\(S_{ADC} = 0.5\cdot 0.5\cdot 10\cdot 10 = 25\)
Ответ: \(а)\: (x-4)^2 + (y-4)^2 =25,\: в)\: 4y = 3x + 29,\:с)\: B (7,0), \:d)\: AB \)-диаметр, \(\:е)\: S_{ADC} = 25\)
3. Дано уравнение прямой \(AB:\: 3y=4x,\)
уравнение прямой \(AC:\: 7y = x + 25\), координата точки \(C\) по \(x\) равна \((-4),\) координата точки \(B\) по \(y\) равна \((-4).\)
а) Найдите координаты точек \(A, B, C.\)
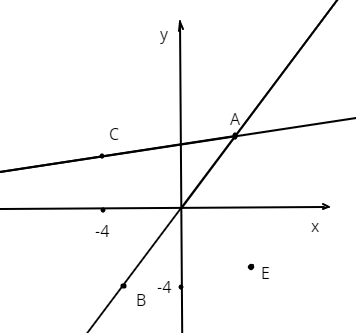
Дана точка \(E\) в четвертой четверти с координатой по оси \(y\) равной \((-3),\:|CE| = 10.\)
в) Найти координату \(x\) точки \(E\).
\(D\) – центр окружности, описанной вокруг \(\triangle ABC\).
с) Найти уравнение окружности.
d) Где находится точка \(E\)? Внутри окружности, вне или на окружности?
е) Найти площадь треугольника \(\triangle ADC\).
а) \((4/3)x = x/7 +25/7 => 25x = 75 => x = 3 => y = 4 =>A(3,4), B(-3,-4), C(-4,3)\)
в) \((3+3)\cdot2 + (4+x)^2= 10^2=> x =4 => E(4,-3)\)
с) \(|OA|^2 = |OC|^2 = |OB|^2 =4^2 + 3^2 = 25\)
Уравнение окружности \(x^2 + y^2 = 25\)
d) Точка \(E\) лежит на окружности
е) \(S_{ACD} = S_{ABC}/2 = (1/4)\cdot |AC| \cdot |CB| , \:|AC| =|CB| , |AC|^2=(4-3)^2 + (3+4)^2 = 50\)
\(S_{ACD}= 12.5\)
Ответ: \(а) \:A(3,4),\: B(-3,-4),\:C(-4,3), \:в) \:E(4,-3,), \:с)\: x^2 +у^2 = 25,\: \) \(d)\)Точка \(E\) лежит на окружности, \(е)\: S_{ACD}=12.5\)
‹
›




