1. Дана функция \(f{{(x)} = {\frac{3}{{({x - 1})}^{2}} - 6}}{x + 6}\)
а) Найти область определения.
в) Найти координаты точек пересечения с осями.
с) Найти координаты точек экстремума и определить их тип, найдите области возрастания и убывания функции.
d) Найдите горизонтальные и вертикальные асимптоты
e) Начертите схематический график функции.
f) Дана функция \(g(x) = f(x)+a\), \(a\)- параметр. Точка экстремума лежит на оси \(x\). Найдите \(a\).
g) Начертите схематичный график \(g(x)\)
h) Найдите площадь фигуры, заключенной между графиком \(g(x)\), прямой \(x = -2\) и осью \(x\).
а) \(x≠1\)
в) \(x=0, y=9 =>(0,9); y=0, x=1.79 => (1.79;0)\)
с) \(f '(x) = (-6)/(x-1)^3-6 = 0, x=0, y=9, (0,9)\)- экстремум, \(x<0, f '(x)<0, f(x)\) убывает, \(x>0, f '(x)>0, f(x)\) возрастает => \((0,9)\) - минимум
d) \(x = 1\) -вертикальная асимптота,
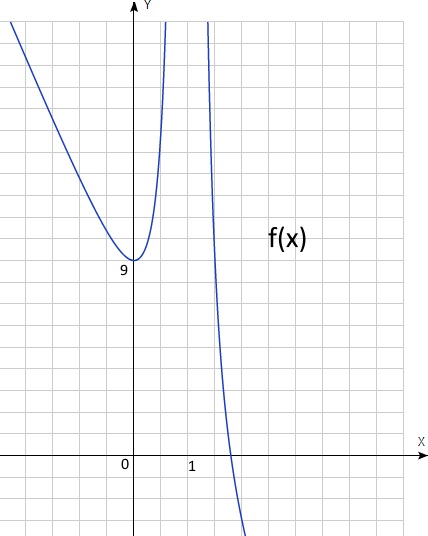
f) \(a=-9\)

h) \({\int g}{(x)}{\mathit{dx} = {\frac{-3}{x - 1} - 3}}{x^{2} - 3}{x + C},{S = {\int\limits_{-2}^{0}g}}{(x)}{\mathit{dx} = {3 - {({1 - 12 + 6})}} = 8}\)
Ответ: а) \(x≠1, \) в)\( (0,9) ; (1.79,0),\) с) \((0,9)\) – экстремум, d) \(x=1\) вертикальная асимптота, f) \(a =-9\) h) \(S = 8\)
2. Дана функция \(f{{(x)} = \frac{\mathit{Cx}^{2}}{{x^{2} - 3}{x + 2}}}\)
а) Найдите область определения.
в) У функции есть горизонтальная асимптота \(у = 2\) . Найдите параметр \(С\)
Для функции с найденным параметром
с) Найдите координаты точек пересечения с осями.
d) Найдите координаты точек экстремума и определите их тип, найдите области возрастания и убывания функции.
е) Найдите горизонтальные и вертикальные асимптоты
f) Начертите схематический график функции.
а) \(x^2-3x+2 = (x-1)(x-2)\) => \(x≠1\) и \(x≠2\)
в) \(lim\)\(х\)→±∞\(Cx^2/(x^2-3x+2)=C\) => \(C = 2 \)
с) \(x =0, y =0 => (0,0)\)
d) \(f '(x) =2Cx(x^2-3x+2)-(2x-3)Cx^2)/(x^2-3x+2)^2=0\) =>\(2x(x^2-3x+2)-(2x-3)x^2=0\) => точки экстремумов \((0,0)\) и \((4/3;-16)\)
\(x<0, f '(x)<0, f(х)\) убывает,
\(0<x< 4/3, f '(x)>0, f(х)\) возрастает,
\(x> 4/3, f '(x)<0, f(х)\) убывает => \((0,0)\)минимум, \((4/3,-16)\) максимум
е) \(y= 2\) горизонтальная асимптота, \(x=1\) и \(x=2\) вертикальные асимптоты
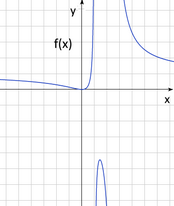
Ответ: а) \(x≠1\) и \(x≠2\), в) \(С = 2\), с)\( (0,0)\), d) \((0,0)\) минимум, \((4/3,-16)\) максимум, е) \(y= 2\) горизонтальная асимптота, \(x=1\) и \(x=2\) вертикальные асимптоты
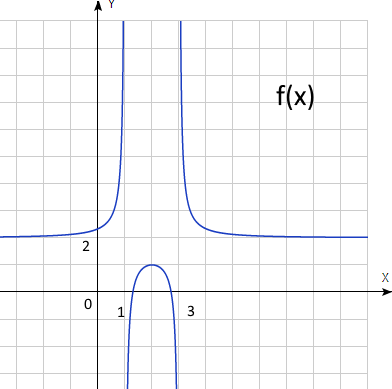
3. Дана функция \(f{{(x)} = {\frac{- 1}{1 - {({x - 2})}^{2}} + C}}\)
а) Найти область определения.
в) Найти координаты точек экстремума и определить их тип, найдите области возрастания и убывания функции.
с) Прямая \(y=1\) является касательной к графику в точке экстремума. Найдите параметр \(С.\)
d) Для функции с найденным параметром найдите горизонтальные и вертикальные асимптоты
e) Начертите схематический график функции.
f) Начертите схематический график \(f '(x) \)- производной функции.
g) Вычислите площадь фигуры, заключенной между графиком \(f '(x)\), прямой \(x =1.5\) и осью \(x\).
а) \(1-(x-2)^2 ≠ 0\) => \(x≠1\) и \(x≠3\)
в) \(f '(x)=(-2)(x-2)/(1-(x-2)^2)^2\) => \(x=2, y = C-1\) => \((2,C-1)\)
так как \((1-(x-2)^2)^2 \geq 0\) производная меняет знак только в точке \(x=2\),
для \(x<2, f '(x)>0 => f(x) \)возрастает, для \(x>2, f '(x)<0 => f(x)\) убывает \(=>(2,С-1)\) максимум
с) \(1 = С-1 => С = 2 => \)\(f{{(x)} = {\frac{- 1}{1 - {({x - 2})}^{2}} + 2}}\)
d) \(x=1\) и \(x=3\) вертикальные асимптоты,
\(lim\)\(х\)→±∞\({\frac{- 1}{1 - {({x - 2})}^{2}} + 2}=2\) =>\( y = 2\) горизонтальная асимптота
f) \(f '{{(x)} = {\frac{- 2(x-2)}{{({3 - x})}^{2}{({x - 1})}^{2}}}}\), \(x<2, f '(x)>0, x>2, f '(x)<0, x=0, f '(x)=4/9, x=2, f '(x)=0, x=1 \)и \(x=3\) вертикальные асимптоты, \(lim\)\(x→±∞\)\(f '(x)=0, y= 0\) горизонтальная асимптота
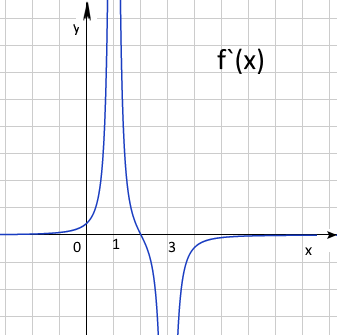
g) \({\int f'}{(x)}{\mathit{dx} = {f(x)}+C}\) => \(S =f(2) - f(1.5) = 1-(2/3) = 1/3 \)
Ответ: а) \( x≠1 \)и \( x≠3\) , в) \((2,С-1)\) максимум, с) \(С = 2\), d) \(x=1 \) и \( x=3\)
вертикальные асимптоты, \(y = 2\) горизонтальная асимптота, g) \(S = 1/3\)
‹
›




