1. Дана функция \(f(x)=(1-x^2)\sqrt{(2-x)}\)
а) Найти область определения.
в) Найти координаты точек пересечения с осями.
с) Найти координаты точек экстремума и определить их тип, найдите
области возрастания и убывания функции.
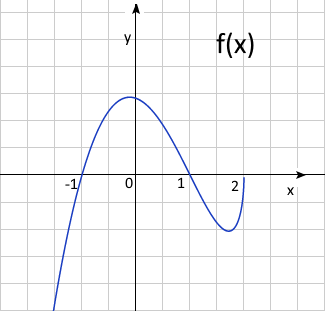
d) Начертите схематический график функции.
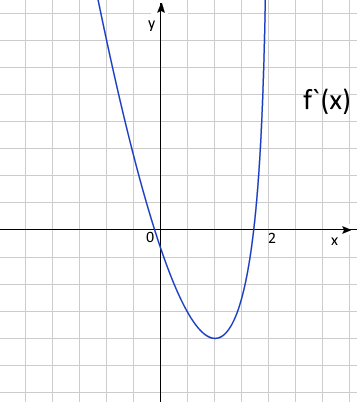
e) Начертите схематический график производной функции.
f) Вычислите площадь фигуры, заключенной между графиком производной
функции\(f'(x)\), прямыми \(x = -2, x = -1\) и осью \(x\).
Решение
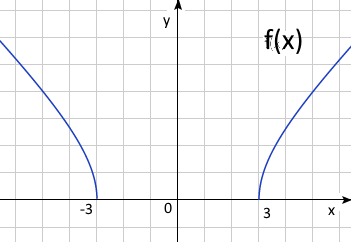
а) \(x ≤ 2\)
в) \(x = 0, y =\sqrt{2} = 1.41=> (0;1.41)\);
\( y= 0, x =-1, x=0, x=1=> (-1,0), (0,0), (1,0)\)
с) \( f'(x) = (5x^2-8x-1)/(2\sqrt{2-x}) =0\), \(x_1 = (4-\sqrt{21})/5 = - 0.12, f(-0.12) = 1.44, x_2 = (4+\sqrt{21})/5 = 1.72, f(1.72) = -1.04\)
\((-0.12; 1.44)\) и \((1.72; -1.04)\) - экстремумы.
Если \(x<-0.12\) или \(1.72<x<2\) тогда \(f'(x)>0\) и \(f(x)\) возрастает,
если \(-0.12<x<1.72 , f'(x)<0\) и \(f(x)\) убывает
\((-0.12, 1.44)\) - максимум, \((1.72, -1.04)\) - минимум
d)
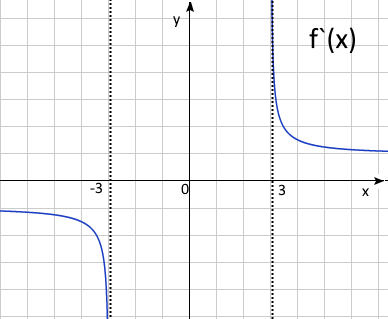
e) \( x=2 \) вертикальная асимптота для \(f'(x)\),
\(x= 0, f'(x) = -0.35; f'(x) =0, x = -0.12\) и \(x = 1.72\)
f) \(\int{f'(x)dx = f(x)+C} => S = f(-1) – f(-2) = 0 - (-3)\cdot 2 = 6\)
Ответ: \(a) x ≤ 2, b) (-1,0), (0,0), (1,0), c) (-0.12, 1.44) \) - максимум,\( (1.72, -1.04)\) - минимум, \( f) S = 6\)
2. Дана функция \(f(х)=\sqrt{(9-x^2)}\)
а) Найдите область определения.
в) Найдите координаты точек пересечения с осями.
с) Найдите координаты точек экстремума и определите их тип, найдите
области возрастания и убывания функции.
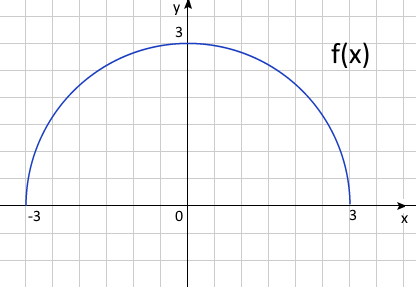
d) Начертите схематический график функции.
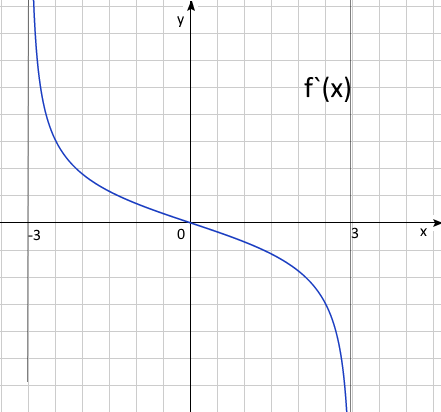
e) Начертите схематический график производной функции.
f) Вычислите площадь фигуры, заключенной между графиком производной
функции \(f'(x)\), прямыми \(x = -2, x = 0\) и осью \(x\).
Решение
а) \(9-x^2≥0, (3-x)(3+x)≥0 => -3≤x≤3\)
в) \(x = 0, y = 3 => (0,3), y = 0, x = 3 \) или \(x = -3 => (-3,0),
(3,0)\)
с) \(f'(x) = (-x)/\sqrt{9-x^2} = 0, x=0\), если \( -3<x<0, f'(x)>0 => f(x)\) возрастает, если \(0<x<3, f'(x)<0 =>, f(x)\)
убывает \(=> (0,3)\) - максимум
е) Для \(f'(x)\) область определения \(-3<x<3, x=-3\) и \(x=3\)
вертикальные асимптоты, \((0,0)\) — точка пересечения с осями, если
\(-3<x<0, f'(x)>0\), если \(0<x<3, f'(x)<0\)
f) \(\int{f'(x)dx} = f(x)+С => S = f(0) – f(-2) = 3 - \sqrt{5} = 0.76\)
3. Дана функция \(f(х)= \sqrt{x^2-9}\)
а) Найдите область определения.
в) Найдите координаты точек пересечения с осями.
с) Найдите координаты точек экстремума и определите их тип, найдите области возрастания и убывания функции.
d) Начертите схематический график функции.
e) Начертите схематический график производной функции.
f) Вычислите площадь фигуры, заключенной между графиком производной
функции \(f'(x)\), прямыми \(x = -2, x = 0\) и осью \(x\).
Решение
а) \(x^2-9≥0, (x-3)(3+x)≥0 => x ≤ -3\) или \(x ≥ 3\)
в) \(y = 0, x = 3\) или \(x = -3 => (-3,0), (3,0)\)
с) \(f'(x) = x/\sqrt{x^2-9} ≠ 0, x≠0\), если \(-∞<x<-3 ,
f'(x)<0 => f(x)\) убывает, если \(3<x<∞ , f'(x)>0 =>f(x)\)
возрастает, экстремума нет.
d)
е) Для \(f'(x)\) область определения \(x<-3\) или \(x >3, x=-3\) и \(x=3\)
вертикальные асимптоты, если \(-∞<x<-3 , f'(x)<0 \), если \(3<x<∞ ,f'(x)>0\)
f) \(\int{f'(x)dx} = f(x)+C => S = f(0) – f(-2) = 3 - \sqrt{5} = 0.76\)
4. Дана функция \(f(x) = x^2\sqrt{1-x}\)
а) Найти область определения.
в) Найдите координаты точек пересечения с осями.
с) Найти координаты точек экстремума и определить их тип, найдите
области возрастания и убывания функции.
d) Начертите схематический график функции.
e) Дана функция \(g(x) = 2-x^2 \sqrt{1-x}\). Найти координаты
точек экстремума и определить их тип.
f) Вычислите площадь четырехугольника с вершинами в точках
экстремумов функций \(f(x), g(x)\).
Решение
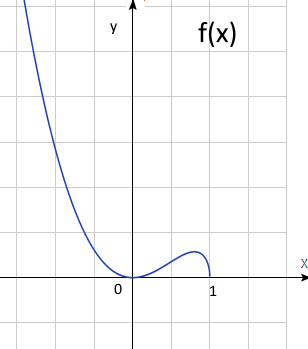
а) \(1-x ≥ 0 => x≤1\)
в) \((0,0), (1,0)\)
с) \( f'(x) = 2x \sqrt{1-x} - x^2 /(2(\sqrt{1-x})= 0 => x = 0 , y = 0\)
или \(x = \frac{4}{5} , y =\frac{16}{25\sqrt{5}}=0.29\)
если \(x<0\) или \(\frac{4}{5}<x<1 , f'(x)<0 => , f(x)\) убывает,
если \(0<x<\frac{4}{5}, f'(x)>0 => f(x)\) возрастает
\((0;0)\) минимум, \((0.8;0.29)\) максимум.
d)
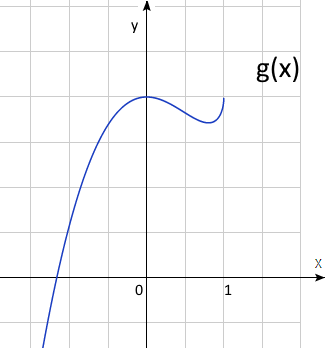
е) Если \(x = \frac{4}{5}\) тогда \(g(x) = 2- \frac{16}{25\sqrt5} = 1.71 => (0,2)\)
максимум, \((0.8, 1.71)\) минимум
f) \(S = \frac{1}{2}\cdot(2+1.71-0.29)\cdot\frac{4}{5}= 1.37\)
‹
›