1. Дана функция \(y= -x^2+6x-5\)
a) Найдите координаты точек пересечения графика функции с осью \(x\)
Прведена прямая параллельная оси \(x\) и пересекающая график функции выше оси \(x\) в точках \(A\) и \(B\)
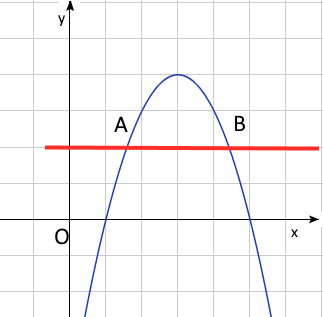
b) Координата по оси \(x\) точки \(A\) равна \(x\). Чему равна координата точки \(B\) по оси \(x\)?
c) \(O\) - точка начал координат. Найдите при каком значении \(x\) площадь \(\triangle ABO\) будет максимальна.
a) \(y=-(x-5)(x-1) =>\) координаты точек пересечения с осью\(x\) \( (1,0)\) \((5,0)\)
b) \(-x^2+6x-5=-x_{B}^2+6x_{B}-5 => x_{B}^2 - x^2=6 \cdot (x_{B}-x) => (x_{B}-x)(x_{B}+x-6)=0\)
\(x_{B}\neq x => x_{B}+x=6 =>x_{B}=6-x\)
c) \(S_{ABO} = 0.5\cdot (-x^2+6x-5)(x_{B}-x)=0.5\cdot (-x^2+6x-5)(6-2x)=x^3-9x^2+23x-15\)
\(S'=3x^2-18x+23=0 => x_{1,2}=(9\pm 2\sqrt{3})/3\),
очевидно, что \(1<x_A<3\) и \(3<(9+ 2\sqrt{3})/3\)
если \( 1<x<(9- 2\sqrt{3})/3\) тогда \(S'> 0\) и \(S(x)\)возрастает, если \((9- 2\sqrt{3})/3 <x < 3\), тогда \(S'<0, S(x)\) убыват
\( => x=(9 - 2\sqrt{3})/3\) точка максимума
Ответ: a) \((1,0)\) , \((5,0)\); b) \( x_{B}=6-x\) ; c) \(x=(9 - 2\sqrt{3})/3\)
2. Дана функция \(y = \frac {1} {x}\)
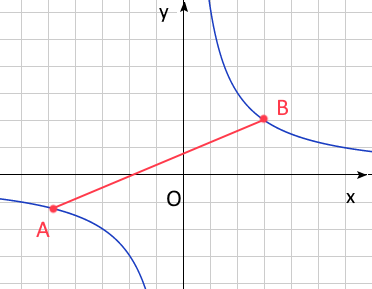
Координата точки \(B\) по оси \(x\) равна \(1\). Обозначим координату точки \(A\) по оси \(x\) через \(x\)
a) Чему равно \(|AB|^2\)?
b) При каком значении \(x\) длина \(|AB|\) минимальна?
3. Дана функция \(y=x^2+3\).
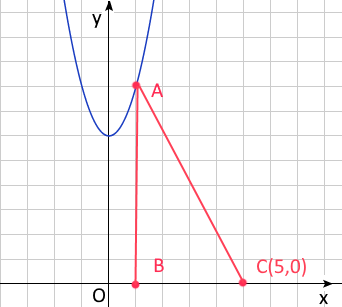
Точка \(A\) лежит на графике функции, точки \(B\) и \(C(5,0)\) на оси \(x\)
Координата точки \(A\) сопадает с координатой точки \(B\) по оси \(x\).
a) Найдите максимальную площадь треугольника \(\triangle ABC\)
b) Найдите минимальную площадь треугольника \(\triangle ABC\)
‹
›


