a) \(|AD|=|AB|/cos(\angle{BAD})=8/cos(67^0)=20.5\)
b) \(|BC|=|AD|-2|AB|cos(\angle{BAD})=20.5-2\cdot8\cdot cos(67^0)=14.2\)
c) \(h=|AB|sin(\angle{BAD})=8sin(67^0)=7.4\)
d) \(P=2|AB|+|AD|+|BC|=50.7\)
1. Дана равнобедренная трапеция \(ABCD\). Сторона \(AB \) перпендикулярна диагонали \(BD\), длина \(CD\) равна \(8\). Угол \(\angle BAD\) равен \(67^0\)
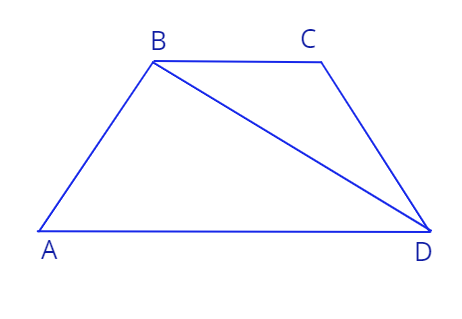
a) Найдите длину основания \(AD\).
b) Найдите длину основания \(BC\).
c) Найдите высоту трапеции.
d) Найдите периметр треугольника \(\triangle BCD\).
2. Дан прямоугольный треугольник \(\triangle ABC\), угол \(\angle ACB\) равен \(90^0\). Длина стороны \(BC\) равна \(30\). Точка \(D\) лежит на стороне \(AC\). Длина отрезка \(BD\) равна \(48\), угол \(\angle ABC\) равен \(68^0\).
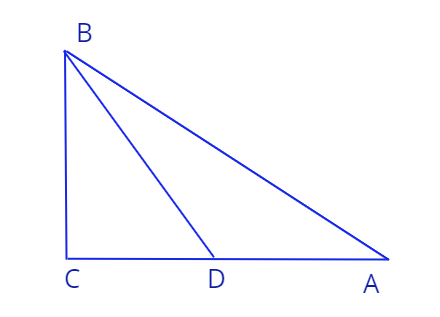
a) Найдите длину гипотенузы \(AB\).
b) Найдите длину катета \(AC\).
c) Найдите угол \(\angle BDC\).
d) Найдите длину отрезка \(AD\).
e) Найдите площадь треугольника \(\triangle ABD\).
a) \(|AB|=|BC|/cos(\angle{ABC})=30/cos(68^0)=80.1\)
b) \(|AC|=|BC|\cdot tan(\angle{ABC})=30\cdot tan(68^0)=74.3\)
c) \(sin(\angle{BDC})=|BC|/|BD|=30/48\;=>\angle{BDC}=38.7^0\)
d) \(|AD|=|AC|-|CD|=|AC|-\sqrt{|BD|^2-|BC|^2}=74.3-\sqrt{48^2-30^2}=36.8\)
e) \(S_{ABD}=(1/2)\cdot |AD|\cdot |BC|=(1/2)\cdot 36.8\cdot 30=552.\)
Ответ:
3. Дан прямоугольник \(ABCD\), точка \(F\) лежит на стороне \(AD\). Длина стороны \(CD\) равна 9, длина отрезка \(DF\) равна \(12\). Угол \(\angle ABF\) равен \(25^0\).
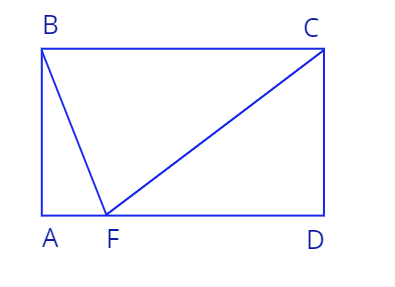
a) Найдите длину отрезка \(CF\).
b) Найдите величину угла \(\angle CFD\).
c) Найдите длину отрезка \(BF\).
d) Найдите периметр треугольника \(\triangle BFC\).
a) \(|CF|=\sqrt{|FD|^2+|CD|^2}=15\).
b) \(tan(\angle CFD)=|CD|/|FD|=0.75\:=>\angle CFD=36.9^0\).
c) \(|BF|=|AB|/cos(\angle ABF)=9.9\).
d) \(P_ {BFC}=|BC|+|CF|+|BF|=|AF|+|FD|+|CF|+|BF|=9\cdot tan(25^0)+12+15+9.9=41.1\).
4. Дан прямоугольный треугольник \(\triangle ABC\), угол \(\angle ACB\) равен \(90^0\). Длина катета \(BC\) равна \(30\). Точка \(D\) лежит на стороне \(AC\), \(BD\) биссектриса угла \(\angle ABC\). Длина катета \(AC\) равна \(40\).
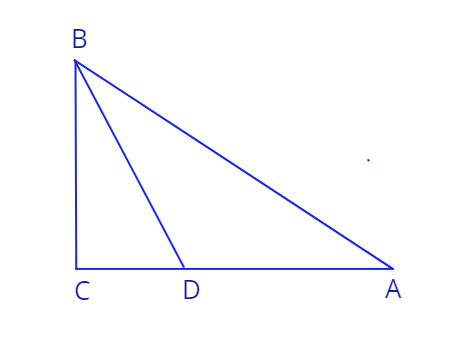
a) Найдите длину гипотенузы \(AB\).
b) Найдите длину отрезка \(CD\).
c) Найдите угол \(\angle BDC\).
d) Найдите длину отрезка \(BD\).
e) Найдите площадь треугольника \(\triangle ABD\).
a) \(|AB|=\sqrt{|BC|^2+|AC|^2}=50\).
b) \(|CD|/|AD|=|BC|/|AB|\:=>|CD|/(|AC|-|CD|)=|BC|/|AB|\:=>|CD|=15\).
c) \(tan(\angle BDC)=|BC|/|CD|=2\:=>\angle BDC=63.4^0\).
d) \(|BD|=\sqrt{|BC|^2+|CD|^2}=33.5\).
e) \(S_{ABD}=(1/2)\cdot |AD|\cdot |BC|=375\).
5. Дан прямоугольник \(ABCD\), точка \(F\) лежит на стороне \(AD\). Длина стороны \(CD\) равна 12, длина отрезка \(DF\) равна \(16\). Угол \(\angle BFC\) равен \(90^0\).
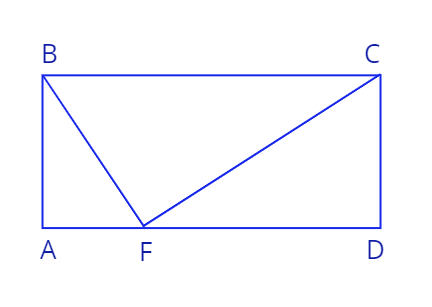
a) Найдите длину отрезка \(CF\).
b) Найдите длину отрезка \(BF\).
c) Найдите длину отрезка \(AF\).
d) Найдите величину угла \(\angle CFD\).
e) Найдите периметр треугольника \(\triangle BFC\).
a) \(|CF|=\sqrt{|DF|^2+|CD|^2}=20\).
b) \(\angle BFC=90^0\:=>\triangle BCF \sim \triangle CDF \sim \triangle ABF\:\) по двум углам \(=>|BF|/|CD|=|CF|/|DF|\:=>|BF|=|CD|\cdot |CF|/|DF|\:=>|BF|=15\).
c) \(|AF|=\sqrt{|BF|^2-|AB|^2}\:=>|AF|=9\).
d) \(tan(\angle CFD)=|CD|/|FD|=0.75\:=>\angle CFD=36.9^0\).
e) \(S_{BFC} = |CF|+|FD|+|CD|=60\).
‹ ›