a) \(ER=RT=TK=KE,\:S_{AEK}=5x-x^2/2,\:\) b) \(x=5,\:\) c) \(S_{min}=50.\)
1. На рисунке показаны графики двух функций \(f(x)=x^2-4x+8, \: g(x)=-x^2+5x-4.\) Отрезок \(AB\) параллелен оси \(y\) и соединяет точки, лежащие на графиках функций \(f(x)\) и \(g(x).\) Точки \(C\) и \(D\) лежат на оси \(y,\) \(ABCD-\) прямоугольник (см. рисунок).
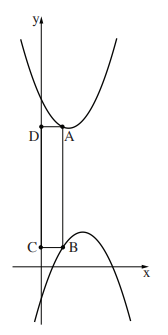
а) Обозначим координату точки \(A\) по оси \(x\) через \(x.\) Выразите с помощью \(x\) координаты точек \(C\) и \(D.\)
в) Выразите с помощью \(x\) длину отрезка \(AB.\)
с) При каком \(x\) периметр прямоугольника будет минимален? Чему равен этот минимальный периметр?
2. На рисунке показан график функции \(f(x)=-x^2-2x+12\) и прямая \(y=5.\) У точки \(A,\) лежащей на графике функции \(f(x),\) координата по оси \(x\) больше нуля, точки \(D\) и \(C\) лежат на оси \(y,\) точка \(B\) лежит на прямой \(y=5, \: ABCD-\) прямоугольник.
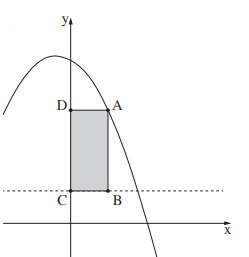
а) Обозначим координату точки \(A\) по оси \(x\) через \(x.\) Выразите с помощью \(x\) координаты точки \(D.\)
в) Выразите с помощью \(x\) длину отрезка \(AB.\)
с) При каком \(x\) площадь прямоугольника \( ABCD-\) будет максимальна? Чему равна эта максимальная площадь?
3. Дан прямоугольник, его стороны равны 3 и 10. Этот прямоугольник разбили двумя перпендикулярными прямыми на четыре прямоугольника (см. рисунок), так что один из них имеет стороны \(x\) и \(2x.\) Сторона длиной \(2x\) лежит на стороне большого прямоугольника с длиной \(10.\)
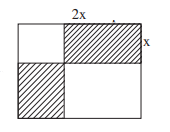
а) Выразите с помощью \(x\) размеры остальных трех прямоугольников.
в) При каком \(x\) суммарная площадь двух прямоугольников, одного, со сторонами \(x\) и \(2x\), и другого, со сторонами \(3-x\) и \(10-2x,\) будет минимальной?
с) Найдите эту минимальную площадь.
4. Дан квадрат \(ABCD\) со стороной равной 10. От его вершин отложены равные отрезки \(AE,\:BR,\:CT,\:DK.\) Точки \(E,R,T,K \) соединены прямыми. Обозначим длину отрезка \(AE\) через \(x.\)
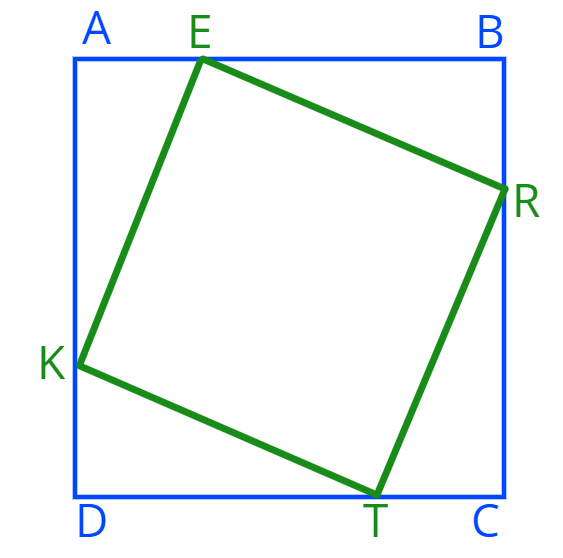
а) Сравните длины отрезков \(ER,\:RT,\:TK,\:KE.\) Выразите с помощью \(x\) площадь треугольника \( \triangle AEK.\)
в) При каком \(x\) площадь четырехугольника \(ERTK\) будет наименьшей?
с) Найдите эту минимальную площадь.
5. Дан круг с радиусом \(R=5.\) В круг вписали прямоугольник \(ABCD.\) Обозначим длину отрезка \(AB\) через \(x.\)
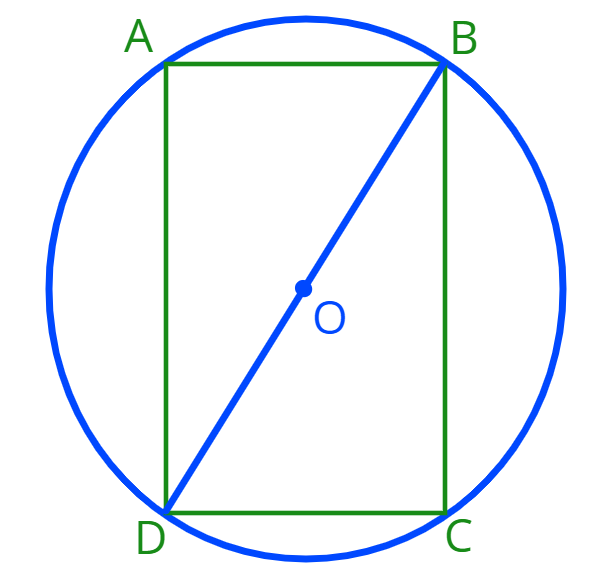
а) Выразите с помощью \(x\) площадь прямоугольника \( ABCD.\)
в) При каком \(x\) площадь прямоугольника \( ABCD\) будет наибольшей?
с) Найдите эту максимальную площадь.
a) \(S_{ABCD}=x\cdot\sqrt{100-x^2},\:\) b) \(x=5\sqrt2,\:\) c) \(S_{max}=50.\)
6. Дан треугольник \(ABC\) с основанием \(|AC|=10\) и площадью \(S_{ABC}=20\). В треугольник вписали прямоугольник \(ERTK.\) Обозначим длину отрезка \(ER\) через \(x.\)
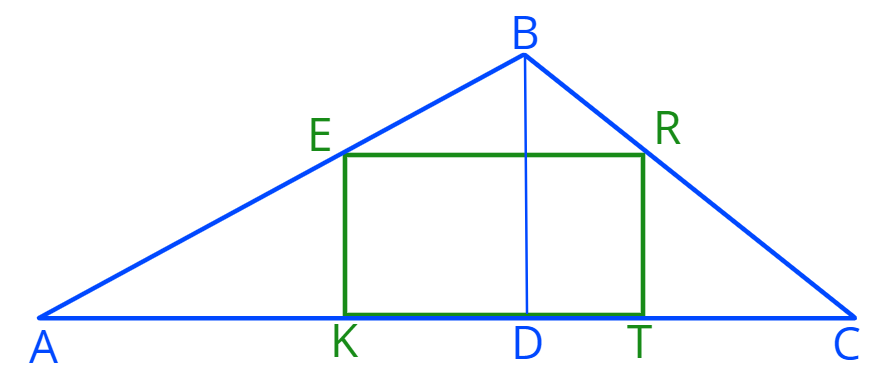
а) Выразите с помощью \(x\) длину стороны \( |EK|.\)
в) При каком \(x\) площадь прямоугольника \( ERTK\) будет наибольшей?
с) Найдите эту максимальную площадь.
a) \(|EK|=4(10-x)/10,\:\) b) \(x=5,\:\) c) \(S_{max}=10.\)
7. Дан прямоугольный лист картона со сторонами 50 и 80. Из этого листа собирают открытую сверху коробку, вырезав у каждого угла по квадрату. Обозначим сторону квадрата через \(x.\)
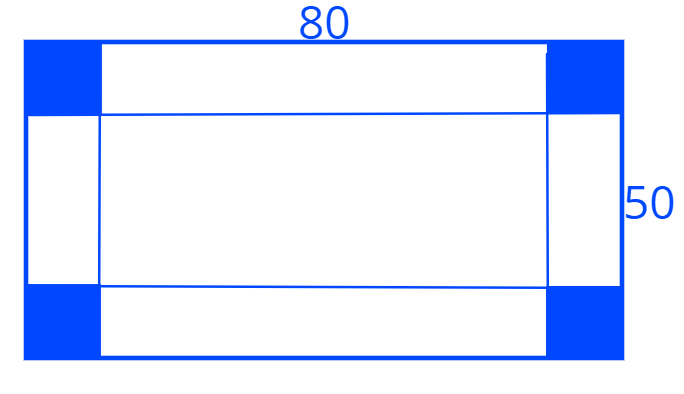
а) Выразите с помощью \(x\) площадь оставщегося после вырезания листа картона.
в) Выразите с помощью \(x\) объем получившейся коробки.
с) Найдите при каком \(x\) объем коробки будет максимален, и определите чему равен этот максимальный объем.
a) \(S=4000-4x^2,\:\) b) \(V=4x^3-260x^2+4000x,\:\) c) \(x=10,\:V_{max}=18000.\)
‹ ›