1. Прямая \(AB,\) уравнение которой \(y=-\frac{4}{3}x+24,\) пересекает ось \(x\) в точке \(A,\) а ось \(y\) в точке \(B.\)
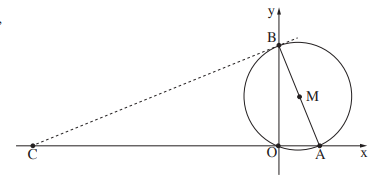
а) Найдите координаты точек \(A\) и \(B.\)
в) Отрезок \(AB\) является диаметром окружности с центром в точке \(M\) (см. рисунок). Найдите координаты точки \(M.\)
с) Найдите длину радиуса и напишите уравнение этой окружности.
d) Через точку \(B\) провели касательную к окружности. Найдите угловой коэффициент этой касательной.
e) Найдите уравнение этой касательной.
f) Касательная пересекает ось \(x\) в точке \(C.\) Найдите координаты точки \(C.\)
g) Найдите площадь четырехугольника \(BCOM,\) \(O-\) точка начала координат.
h) Найдите площадь треугольника \(CMA.\)
2. Дана окружность с центром в точке \(M(16,24).\) Точка \(A(7,36)\) лежит на этой окружности.
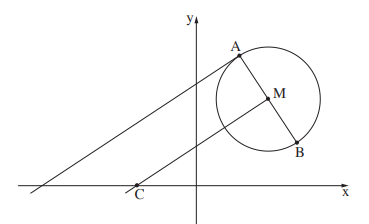
а) Найдите радиус этой окружности.
в) Напишите уравнение окружности.
с) Найдите координаты точки \(B,\) если \(AB-\) диаметр этой окружности.
d) Через точку \(A\) провели касательную к этой окружности. Найдите угловой коэффициент этой касательной.
e) Через центр окружности провели прямую, параллельную данной касательной. Эта прямая пересекает ось \(x\) в точке \(C.\) Найдите уравнение прямой \(MC.\)
f) Найдите координаты точки \(C.\)
g) Найдите площадь треугольника \(AMC.\)
3. Дана окружность с центром в точке \(M\) (см. рисунок) и диаметром \(AC,\) точка \(C\) лежит на оси \(x.\) Хорда \(BC\) лежит на прямой \(y=-\frac{x}{2}+8.\)
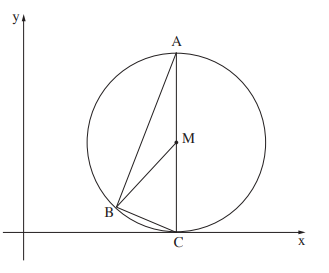
а) Найдите координаты точки \(C.\)
в) Диаметр \(AC\) перпендикулярен оси \(x, \:|AC| = 12,\) найдите координаты точки \(A.\)
с) Найдите уравнение этой окружности.
d) Найдите уравнение прямой, на которой лежит хорда \(AB.\)
e) Найдите координаты точки \(B.\)
f) Найдите площадь треугольника \(BMA.\)
4. Дана окружность с центром в точке \(O_1(3,2).\) Вторая окружность с центром в точке \(O_2(9,-6)\) касается первой в точке \(M(6,k),\) где \(k\) - параметр.
a) Найдите значение \(k.\)
b) Напишите уравнения окружностей.
c) Через точку \(M\) провели общую касательную к окружностям. Напишите уравнение этой касательной.
d) Точка \(P(10,r)\) лежит на этой общей касательной. Найдите значение параметра \(r.\)
e) Через точку \(O_1\) провели прямую, параллельную оси \(y.\) Найдите координаты точек \(K\) и \(T\) - точек пересечения этой прямой с первой окружностью.
f) Во сколько раз площадь треугольника \(PKT\) больше площади треугольника \(PO_1O_2?\)
‹ ›