1. Дан треугольник \(ABC,\) стороны которого заданы уравнениями: \(y=x-4-\) прямая \(AB, y=(-1/7)x-(4/7) -\) прямая \(AC,\) точка \(C\) лежит на оси \(x.\)
а) Найдите координаты вершины \(C.\)
в) Найдите координаты вершины \(A.\)
с) Координата вершины \(B\) по оси \(x\) равна \(28,\) найдите координату \(y\) вершины \(B.\)
d) Найдите уравнение стороны \(BC.\)
e) Через вершину \(A\) и точку \(E -\) точку пересечения \(BC\) с осью \(y\) провели прямую. Найдите координаты точки \(E\) и угол между прямыми \(AE\) и \(BC.\)
f) Найдите площадь треугольника \(AEC.\)
2. Дан четырехугольник \(ABCD\) с вершинами в точках \(A(4,1),\) \(B(8,4),\) \(D(9, - \frac {3} {2} ).\) Сторона \(AB\) перпендикулярна стороне \(BC.\)
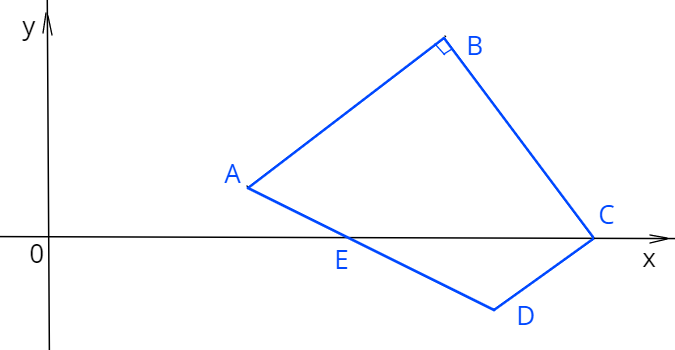
а) Найдите угловой коэффициент стороны \(AB\) и уравнение стороны \(BC.\)
b) Точка \(C\) лежит на оси \(x,\) найдите ее координаты.
с) Найдите координаты точки \(E\) - точки пересечения стороны \(AD\) с осью \(x.\)
d) Покажите, что сторона \(DC\) перпендикулярна стороне \(BC.\)
е) Во сколько раз сторона \(DC\) меньше стороны \(AB?\)
f) Найдите площади треугольников \(ADC\) и \(BDC.\)
3. Дан четырехугольник \(ABCD,\) диагональ \(BD\) перпендикулярна диагонали \(AC,\) координаты вершины \(B\) равны \((1,1).\) Диагональ \(AC\) задана уравнением \(y=-2x+9.\)
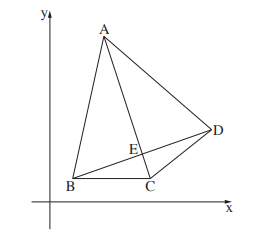
а) Координата вершины \(A\) по оси \(x\) равна \(2,\) найдите ее координату по оси \(y\) и уравнение прямой \(AB.\)
b) Найдите координаты точки пересечения диагоналей.
с) Сторона \(BC\) параллельна оси \(x,\) найдите координаты точки \(C.\)
d) Координата точки \(D\) по оси \(y\) равна \(3\) найдите ее координату по оси \(x.\)
е) Напишите уравнения прямых \(AD\) и \(CD.\)
f) Во сколько раз длина стороны \(CD\) меньше длины диагонали \(AC?\)
4. Дан треугольник \(ABC\) с вершинами \(A(4,-2),\:B(-1.5,k), \:C(r,7),\) где \(k,r\) - параметры. Сторона \(BC\) лежит на прямой \(3y=4x+3.\)
a) Найдите значения параметров \(k,r\) и длину стороны \(BC.\)
b) Через точку \(A\) провели прямую, перпендикулярную прямой \(BC.\) Найдите уравнение этой прямой и координаты точки \(D\) - точки ее пересечения с прямой \(BC.\)
c) Чему равны длина отрезка \(AD\) и площадь треугольника \(ABC?\)
d) Во сколько раз площадь треугольника \(ADC\) больше площади треугольника \(ADB?\)
e) Найдите координаты середины отрезка \(BC.\)
f) Напишите уравнение прямой, проходящей через точку \(A,\) если известно, что эта прямая делит площадь треуголника \(ABC\) на две равные части.
‹ ›