1. Дана функция \(f(x)=x^3-27x+4\)
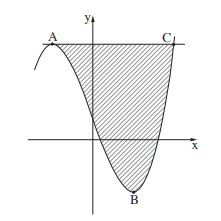
а) Найдите координаты точек экстремума и определите их тип.
в) Найдите уравнение касательной к графику функции, проведенной в точке максимума.
с) Покажите, что координаты точки пересечения этой касательной с графиком функции равны \((6,58).\)
d) Найдите площадь фигуры, заключенной между графиком функции и данной касательной.
2. Дана функция \(f(x)=3x^2-12x+12\) и прямая \(y=2x+1\)
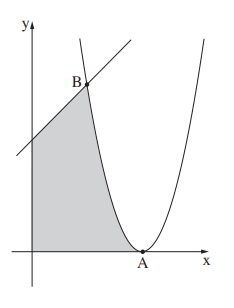
а) Найдите координаты точек пересечения графика функции \(f(x)\) с данной прямой.
в) Найдите координаты точки пересечения графика функции \(f(x)\) с осью \(x.\)
с) Найдите площадь фигуры, заключенной между графиком функции \(f(x)\), данной прямой и осями координат.
3. Дана функция \(f(x)=-2x^2+16x-14.\) График этой функции пересекает ось \(x\) в точках \(A\) и \(B.\) В точке \(C\) с координатой \(x=5\) провели касательную к графику функции \(f(x).\)
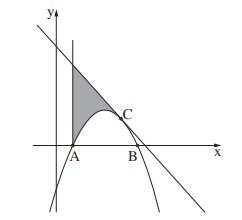
а) Найдите координаты точек \(A,\) \(B\) и \(C.\)
в) Найдите уравнение касательной, проведенной в точке \(C\) к графику функции \(f(x).\)
с) Найдите площадь фигуры, заключенной между графиком функции, касательной и перпендикуляром к оси \(x,\) проведенным через точку \(A.\)
4. Дана функция \(f(x)=2x^2-4x+8.\) Через точку с координатой \(x=2\), лежащую на графике функции \(f(x)\), провели касательную.
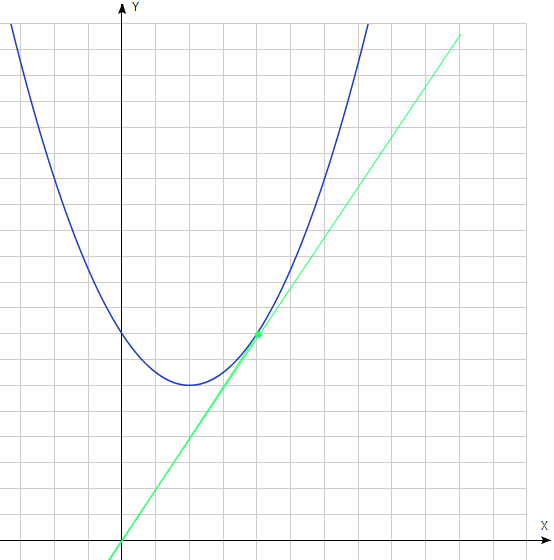
а) Найдите координаты вершины параболы.
в) Найдите уравнение касательной, проведенной в точке с координатой \(x=2\) к графику функции \(f(x).\)
с) Найдите площадь фигуры, заключенной между графиком функции, касательной и осью \(y.\)
5. Дана функция \(f(x)=2x^2-4x+8.\) В точке экстремума и в точке с координатой \(x=2\), лежащей на графике функции \(f(x)\), провели касательные.
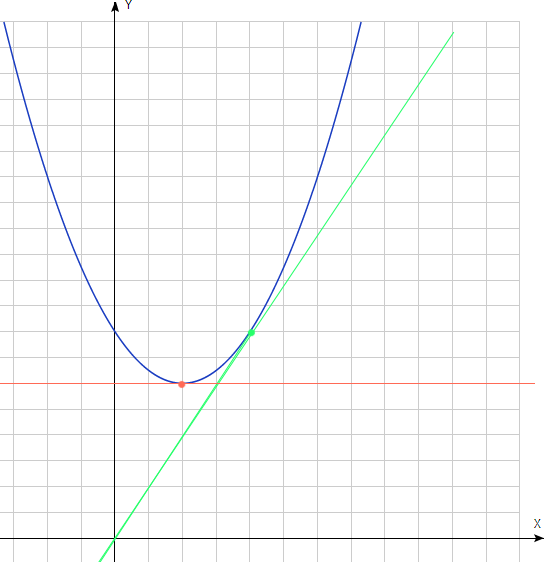
а) Найдите координаты точки экстремума \(f(x)\).
в) Найдите уравнения касательных, проведенных в точке с координатой \(x=2\) и в точке экстремума к графику функции \(f(x).\)
с) Найдите площадь фигуры, заключенной между графиком функции, касательными, проведенными в точке с координатой \(x=2\) и в точке экстремума к графику функции \(f(x).\)
6. Дана функция \(f(x)=x^2-6x+8.\)
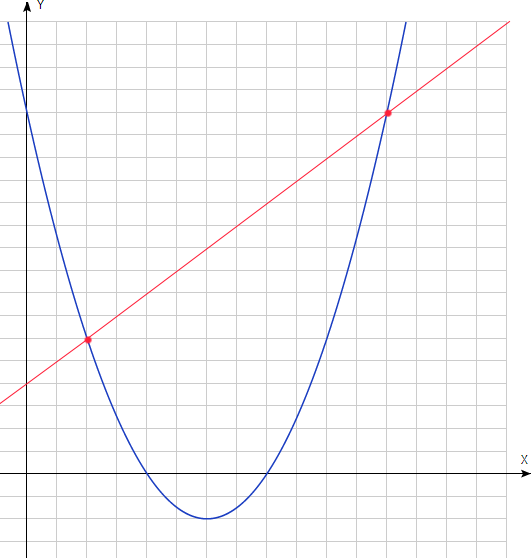
а) Найдите координаты вершины параболы.
в) Через точки с координатами \(x=1\) и \(x=6\), лежащие на графике функции \(f(x)\), провели прямую. Найдите уравнение этой прямой.
с) Найдите площадь фигуры, заключенной между графиком функции и прямой, проведенной через точки с координатами \(x=1\) и \(x=6\).
7. Дана функция \(f(x)=x^2-6x+8.\)
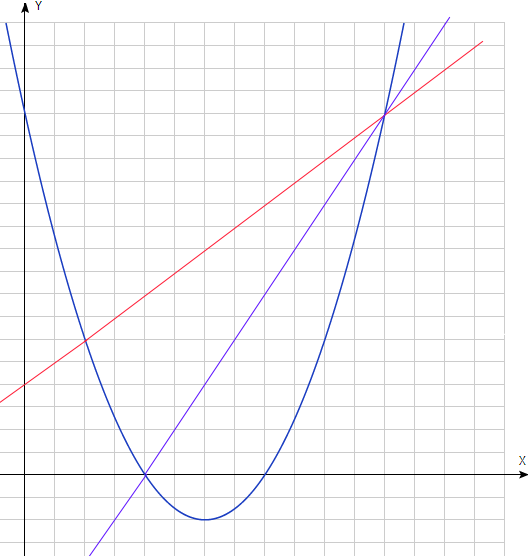
а) Найдите координаты вершины параболы.
в) Через точки, лежащие на графике функции, с координатами \(x=1\) и \(x=6\) провели прямую. Найдите уравнение этой прямой.
c) Через точки с координатами \((2,0)\) и \((6,8)\) провели вторую прямую. Найдите уравнение этой прямой.
d) Найдите площадь фигуры, заключенной между графиком функции и прямыми из пунктов в) и с).
‹ ›