а) \(6\sqrt3\)
в) \(|AD|=6,\:|AB|=4\sqrt3\)
c) \(|BF|=\sqrt{57}\)
d) \(tan\angle EBF=3/\sqrt{19}\)
e) \(tan\angle FB'A=\sqrt{3/52}\)
1. Дан прямоугольный параллелепипед \(ABCDA'B'C'D',\) \(ABCD - \:\) прямоугольник, \(|AD'| = 12,\) угол между проямой \(AD'\) и основанием \(ABCD\) равен \(60^0.\)
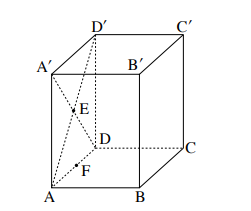
а) Найдите высоту параллелепипеда.
в) Найдите длины сторон основания \(|AD|\) и \(|AB|,\) если объем пирамиды равен \(432.\)
с) Точка \(E\) - точка пересечения диагоналей \(AD'\) и \(DA',\) точка \(F\) середина стороны \(AD.\) Найдите длину отрезка \(BF.\)
d) Найдите угол между прямой \(EB\) и основанием \(ABCD.\)
e) Найдите угол между прямой \(FB'\) и боковой гранью \(CDD'C'.\)
2. У пирамиды \(SABCD\) боковые ребра равны между собой, основание \(ABCD-\) прямоугольник, \(BC=5,\:\) \(AB=8,\:\) объем пирамиды равен \(160.\)
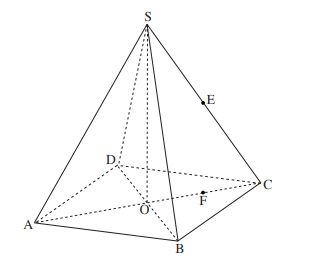
а) Найдите высоту пирамиды \(SO.\)
в) Найдите угол между боковым ребром и основанием пирамиды.
с) Найдите длину бокового ребра.
d) Точка \(F\) лежит на диагонали \(AC,\) точка \(E-\) середина ребра \(SC,\) \(EF \perp AC.\) Найдите длину \(EF\) и угол между прямой \(AE\) и основанием пирамиды.
e) Найдите угол между прямой \(SO\) и боковой гранью \(ADS.\)
а) \(|SO|=12\)
в) \(tan\angle SCO=24/\sqrt{89}\)
c) \(\sqrt{665}/2\)
d) \(|EF|=6,\:\:tan\angle EAF'=8/\sqrt{89}\)
e) \(tan(\alpha)=1/3\)
3. У пирамиды \(SABCD\) боковые ребра равны между собой, основание \(ABCD-\) прямоугольник, угол \(\angle AOD = 40^0,\) высота пирамиды \(SO\) (см. рисунок), \(|SO|=|AB|, \:|AB| > |BC|.\)
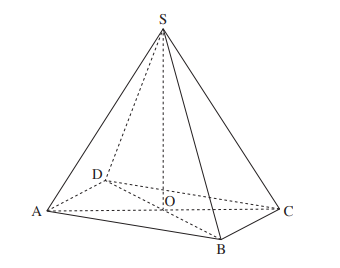
а) Во сколько раз сторона \(AB\) больше \(BC?\)
в) Чему равен угол между боковым ребром и основанием пирамиды?
с) Найдите угол \(\angle ASC\)
d) Найдите длину \(|BC|,\) если площадь треугольника \(ASC\) равна \(14.\)
e) Точка \(E\) середина бокового ребра \(DS,\) найдите объем пирамиды \(EABCD.\)
а) \(|AB|/|BC|=ctan(20^0)\)
в) \(tan\angle SBO=2\cdot cos(20^0)\)
c) \(\angle ASC=2\cdot(90^0-\angle SBO)\)
d) \(|BC|=2tan(20^0)\cdot\sqrt{7cos(20^0)}\)
e) \(V=(28/3)\cdot sin(20^0)\sqrt{7cos(20^0)}\)
4. У пирамиды \(SABCD\) боковые ребра равны между собой, основание \(ABCD-\) прямоугольник, \(BC=2,\:\) \(AB=6,\:\ SC = 4.\)
а) Найдите длину диагонали основания пирамиды.
в) Найдите угол между боковым ребром и основанием пирамиды.
с) Найдите площадь треугольника \(ASC.\)
d) Найдите углы при вершинах всех боковых граней пирамиды и площадь боковой поверхности пирамиды.
e) Найдите угол между прямой \(OS\) и боковой гранью \(ADS.\)
а) \(2\sqrt{10}\)
в) \(cos\angle SCO=\sqrt{10}/4\)
c) \(S_{ASC}=2\sqrt{15}\)
d) \(cos\angle SBA=3/4,\: cos\angle SCB=1/4,\:\angle ASB=180^0-2\angle SBA,\: \angle BSC=180^0-2\angle SCB\)
e) \(tan(\alpha)=\sqrt{3/2}\)
5. Дана прямая призма \(ABCA'B'C'\), в основании которой лежит прямоугольный равнобедренный треугольник \(ABC, |AB|=|BC|.\) Высота призмы равна \(8\), а длина гипотенузы основания равна \(\:4\sqrt 2.\)
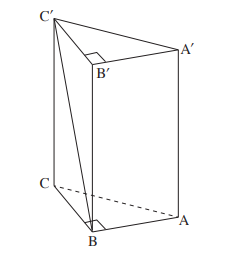
а) Найдите угол между диагональю боковой грани \(BB'C'C\) и основанием призмы.
в) Найдите угол \(\angle AC'B.\)
с) Найдите площадь треугольника \( AC'B.\)
d) Точка \(D\) середина стороны \(CB,\) найдите длину отрезка \(A'D\)
e) Найдите площадь треугольника \(A'CD.\)
а) \(tan\angle C'BC=2\)
в) \(tan\angle AC'B=\sqrt{1/5}\)
c) \(S_{AC'B}=8\sqrt5\)
d) \(|A'D|=2\sqrt{21}\)
e) \(S_{A'CD}=4\sqrt5\)
‹ ›