а) \(B(1,0),\:C(3,0),\:\:x-1=3x-9\:=>x=4\:=>A(4,3).\)
в) \(|BC|=2\)
c) \(S=(1/2)\cdot|BC|\cdot y_a=3\)
Ответ: \(B(1,0),\:C(3,0),\:A(4,3), |BC|=2, S=3.\)
1. Даны уравнения прямой \(AB: \:y=x-1\) и прямой \(AC: \: y=3x-9,\) точки \(B, \:C\) лежат на оси \(x,\) точка \(A\) является точкой пересечения данных прямых.
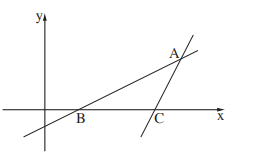
а) Найдите координаты точек \(A,\:B,\:C.\)
в) Найдите длину отрезка \(BC.\)
c) Найдите площадь треугольника \(\triangle ABC.\)
2. Дано уравнение прямой \(AC: \: y=-2x+4.\) Точка \(A\) лежит на оси \(y.\) Эта прямая пересекает ось \(x\) в точке \(B,\) причем \(|AB|=|BC|.\)
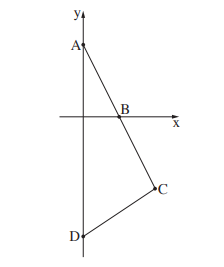
а) Найдите координаты точек \(A, \:B, \:C\)
в) Угловой коэффициент прямой \(DC\) равен \(\frac{3}{4}.\) Найдите уравнение прямой \(DC.\)
c) Точка \(D\) лежит на оси \(y.\) Найдите координаты точки \(D.\)
d) Найдите площадь треугольника \(\triangle ABD.\)
а) \(A(0,4),\:B(2,0),\:C(4,-4).\)
в) \(y=(3/4)x+b,\:=>-4=(3/4)\cdot4+b\:=>b=-7\:=>y=(3/4)x-7.\)
c) \(D(0,-7).\)
d) \(S_{ACD}=(1/2)\cdot|AD|\cdot x_c=(1/2)\cdot 11\cdot4 =22,\:S_{ABD} =(1/2)S_{ADC}=11.\)
Ответ: \(A(0,4),\:B(2,0),\:C(4,-4),\:y=(3/4)x-7,\:D(0,-7),\:S_{ABD}=11. \)
3. Дан параллелограмм \(ABCD.\) Диагональ \(AC\) лежит на прямой \(y=0,5x-1,\) точки \(A\) и \(D\) лежат на оси \(x,\) координаты точки \(B\) равны \((3,3).\)
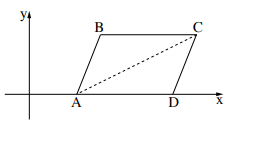
а) Найдите координаты точек \(A,\:C.\)
в) Найдите уравнение прямой \(AB.\)
c) Найдите длину стороны \(BC\) и координаты точки \(D.\)
d) Найдите площадь треугольника \(\triangle ABD.\)
а) \(A(2,0),y_C=y_B=3\:=>x_C=(3+1)/0.5=8\:=>C(8,3).\)
в) \(y=mx+b,\:0=2m+b,\:3=3m+b\:=>m=3,\:b=-6\:=>y=3x-6.\)
c) \(|BC|=8-3=5,\:|BC|=|AD|\:=>x_D=x_A+|BC|=2+5=7\:=>D(7,0).\)
d) \(S_{ABD}=(1/2)\cdot |AD|\cdot y_B=(1/2)\cdot 5\cdot 3=7.5.\)
Ответ: \(A(2,0),\:C(8,3),\:y=3x-6,\:|BC|=5,\:D(7,0),\:S_{ABD}=7.5.\)
‹ ›