a) С момента \(t_0=0\) и до момента \(t=T\) в рамке идет ток, b) \(A\Rightarrow D\Rightarrow C\Rightarrow B,\:\) c) \(Ф=(1/2)Bv^2t^2,\:\) d) \(\varepsilon=Bv^2t,\:\: I=Bv^2t/R,\:\) e) нет, f) \(\overrightarrow{CA}, \overrightarrow{F}\) соноправлены, g) \(F\sim t^2,\:\) h) \(F_{вн}=B^2v^3t^2/R,\:\) i) \(Q=A_{F_{вн}}=В^2v^4T^3/(3R)\)
1. Магнитное поле с индукцией \(B\) ограничено контуром \(KMN\), вектор индукции перпендикулярен экрану. Квадратная рамка из проводника с полным сопротивлением \(R\) движется с постоянной скоростью \(v\) так, как показано на рисунке. В момент времени \(t_0=0\) точка \(C\) достигает точки \(M,\) а в момент времени \(t=T\) точка \(A\) достигает точки \(M.\)
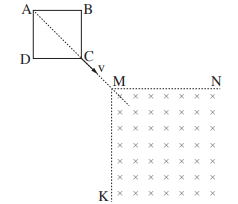
a) Когда в рамке возникает ток, и когда он прекращается?
b) Как направлен ток в рамке?
c) Выразите магнитный поток через рамку как функцию времени, используя параметры \(B,\:v.\)
d) Найдите \(\varepsilon\) индукции, возникающую в рамке, и силу тока в проводнике.
e) Был ли промежуток времени, когда сила тока в проводнике была постоянной?
f) Куда направлена сила, действующая на рамку в интервале времени \((t_0,T)?\)
g) Меняется эта сила или остается постоянной по мере продвижения рамки в область магнитного поля?
h) Какую внешнюю силу надо приложить к рамке, и при движении на каком участке надо ее приложить, для того, чтобы рамка двигалась с постоянной скоростью? Куда надо направить внешнюю силу?
i) Какое количество теплоты выделилось в рамке во время движения? Какую работу совершила внешняя сила при движении рамки?
2. По двум гладким горизонтальным параллельным рельсам \(S_1-S_2\) и \(P_1-P_2\), соединенным через сопротивление \(R=4\Omega\), расстояние между которыми равно \(l=0.5m\), скользит премычка \(MN\), с нулевым сопротивлением и массой \(m=0.1kg\), с постоянной скоростью \(v=2m/s\) (см. рисунок). Между рельсами есть два участка с магнитными полями \(B_1\) и \(B_2\), вектора магнитной индукции которых равны по величине \(|B_1|=|B_2|=0.04T\), противоположно направлены и перпендикулярны плоскости рисунка. Протяженность каждого участка равна \(h=0.4m.\)
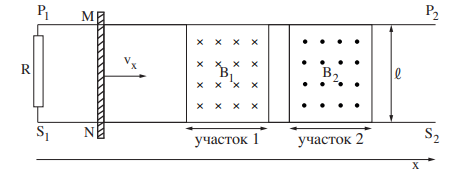
a) Куда направлен и чему равен ток через перемычку при движении на участке 1 и на участке 2?
b) Какую по величине и направлению внешнюю силу надо приложить к перемычке на участке 1 и на участке 2, чтобы перемычка продолжала двигаться с постоянной скоростью?
c) Чему равно количество теплоты, выделившейся на резисторе за время движения перемычки по участку 1?
d) Чему равна работа внешней силы, действующей на перемычку, за время движения перемычки по участку 1?
e) Предположим, что в новом эксперименте на участке 2 к перемычке приложили такую внешнюю силу, что перемычка стала двигаться равноускоренно, с постоянным ускорением \(a=0.2\frac{m}{c^2}\). Чему равна в этом случае сила тока в перемычке, как функция времени?
f) Чему равна в этом случае работа внешней силы, действующей на перемычку, и количество теплоты, выделившейся на резисторе, за время движения перемычки по участку 2?
g) Если увеличить в два раза скорость движения перемычки по участку 1, как изменится заряд, проходящий через перемычку за время движения по участку 1?
a) \(I=Bvl/R=0.01A,\:\) b) \(F=IBl=0.2\cdot10^{-3}N,\:\) c) \(Q=B^2l^2vh/R=8\cdot10^{-5}Дж,\:\) d) \(A=Q\) e) \(I=Bl(v+at)/R,\:\) f) \(Q=(Bl)^2(v^2T+avT^2+a^2T^3/3)/R=0.77\cdot10^{-4}Дж,\:A=Q+ma(vT+aT^2/2)=8\cdot10^{-3}Дж,\:\)где \(T-\) время прхождения участка 2.
3. Ось \(x\) направлена в сторону читателя и перпендикулярна плоскости рисунка. Магнитное поле \(\overrightarrow B\) параллельно оси \(x,\:\: B_x(x)=B_{0}-k\cdot x.\) Проводящее кольцо c полным сопротивлением \(R\) и с диаметром \(D\) помещают в точку \(x=0\), плоскость кольца перпендикулярна оси \(x\). Кольцо приводят в движение с постоянным ускорением \(a\) в направлении оси \(x\), ориентация плоскости кольца не изменяется.
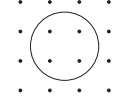
a) Течет ли ток по кольцу во время его движения?
b) Напишите выражения, не подставляя числовые значения, для магнитного потока через кольцо, для \(\varepsilon\) индукции и для силы тока в кольце как функций от времени.
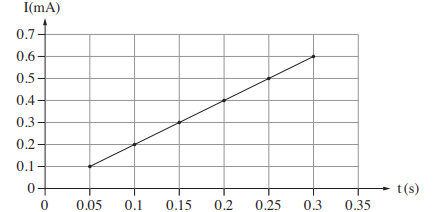
c) На графике представлена зависимость силы тока в кольце от времени. Найдите диаметр кольца, если известно, что \(R=0.04\Omega,\: a=2\frac{m}{c^2},\:k=0.02\)
d) Напишите выражение для силы натяжения, с которой растянуто кольцо в точке с координатой \(x.\)
e) Меняется ли направление тока в кольце в процессе движения? Куда направлен ток в момент времени \(t=0.3c?\)
f) Если ускорение \(a\) в момент времени \(t=0.3s\) станет равным нулю, будет ли течь ток по кольцу?
g) Если в точке \(x=0\) кольцо повернуть на \(180^0\) вокруг диаметра, какой заряд протечет по кольцу?
a) да b) \(Ф=(B_0-kat^2/2)\cdot \pi D^2/4,\:\varepsilon =kat\cdot \pi D^2/4,\:I=kat \cdot \pi D^2/(4R),\:\) c) \(5cm,\:\) d) \(F=k\cdot\pi D^3\sqrt{2ax}(B_0-kx)/(8R),\:\) e) нет, против часовой стрелки, f) будет, g) \(Q=\pi D^2B_0/(2R)\)
4. На рисунке изображен ускоритель заряженных частиц. В прямоугольной области \(C\) нет магнитного поля, есть только электрическое. За пределами области \(C\) электрическое поле отсутствует. Это электрическое поле меняет свое направление в нижней половине области \(C\) на противоположное, оставаясь постоянным по величине. Это поле ускоряет частицы. На рисунке показана траектория протона в области магнитного поля.
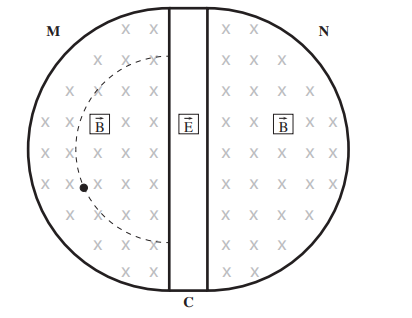
a) Куда направлена скорость протона? Как меняется скорость протона при движении в области магнитного поля.
b) Как связан радиус траектории со скоростью частицы?
c) Напишите выражение для времени пролета \(T/2\) через одну область магнитного поля.
d) Меняется ли со временем время пролета области \(C?\)
e) По какой траектории движутся частицы в ускорителе? Сделайте рисунок.
f) Измерили зависимость скорости протона от времени при его движении через области \(M,C,N\), результаты приведены на графике. Чему равна индукция магнитного поля, если масса протона равна \(m=1.67\cdot 10^{-27}kg,\) а заряд \(q=1.6\cdot10^{-19}C?\)
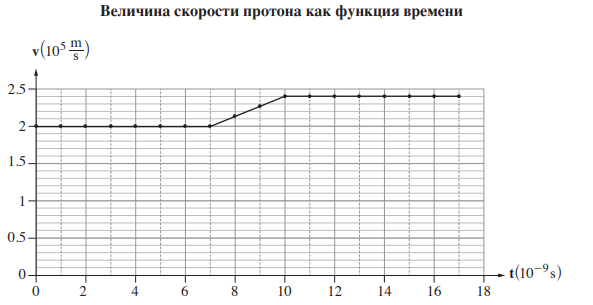
g) Чему равна напряженность электрического поля?
h) Как меняется сила, действующая на протон, со стороны магнитного поля со временем?
a) против часовой стрелки, b) \(R=mv/(qB),\:\) c) \(T/2=\pi m/(qB),\:\) d) да, e) по спирали f) \(B=4.7T,\:\) g) \(E=174\cdot 10^3V/m.\:\) h) \(F=qvB,\:\) сила растет.
5. Дано жесткое проволочное кольцо массы \(m=2gr\) и диаметра \(d=8cm\) и жесткая квадратная проволочная рамка массы \(m=2gr\) со стороной \(l=5cm.\)
a) Рамку положили на горизонтальную непроводящую поверхность. Рамка находится в однородном магнитном поле \(B=0.5T\), линии индукции которого горизонтальны. Какой силы ток надо пустить по рамке, чтобы она начала подниматься?
b) Ось, проходящая через центры двух противоположных сторон квадратной рамки, параллельна длинному прямому проводнику, по которому протекает ток. По рамке пропускают ток. Какое положение займет рамка? Сделайте рисунок, укажите на рнисунке направление токов в проводнике и в рамке.
c) Рамку с током \(I=0.4A\) расположили в одной плоскости с длинным прямым проводником, по которому протекает ток \(I_0=5A.\) Ближайшая к проводнику сторона рамки параллельна ему и удалена от проводника на расстояние \(h=5cm.\) Найдите направление и величину силы, действующей на рамку. (\(\mu_0=4\pi\cdot10^{-7}T\cdot m/A\))
d) Кольцо, по которому протекает ток \(I=0.3A,\) повернули на \(90^0\), теперь плоскость кольца перпендикулярна манитному полю \(B=0.5T\). Найдите силу натяжения в кольце, вызванную магнитным полем.
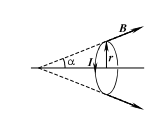
e) Кольцо с током \(I=0.3A,\) поместили в магнитное поле, такое, что в каждой точке кольца поле \(B=0.5T\) образует угол \(\alpha =30^0\) c осью кольца (см. рисунок). Найдите величину и направление полной магнитной силы, действующей на кольцо.
a) \(I=mg/(2Bl)=0.4A,\:\)c) \(F=\mu_0I_0Il^2/(2\pi h(h+l))=2\cdot10^{-7}N\) d) \(F=IBd/2=0.6\cdot10^{-2}N,\:\) e) Сила направлена влево, \(F=IB\cdot\pi d\cdot sin\alpha=1.88\cdot10^{-2}N.\:\)
6. Проводник массы \(m=200gr\) лежит на горизонтальных рельсах перпендикулярно им, расстояние между рельсами равно \(L=60cm.\) Рельсы расположены в однородном горизонтальном магнитном поле с индукцией \(B=0.1T\). Вектор индукции поля параллелен рельсам.
a) По проводнику пропустили ток \(I=20A.\) Для того, чтобы сдвинуть проводник, в направлении, противоположном направлению вектора \(B,\) надо приложить силу\(F_1=0.5N.\) Какую силу надо приложить к проводнику, чтобы сдвинуть его, если направление тока поменять на противополжное? (Две возможности.)
b) Изменили направление магнитного поля, теперь оно направлено вертикально, \(B=0.1T\). Какой силы ток надо пустить по проводнику, чтобы проводник начал двигаться, если коэффициет трения равен \(\mu = 0.6\)?
c) Рельсы подняли так, что они составляют угол \(\alpha\) с горизонтом, \(tg\alpha = 1/2\). Магнитное поле \(B=0.1T\) перпендикулярно плоскости рельсов. Какой силы ток надо пустить по проводнику, чтобы проводник начал двигаться, если коэффициет трения равен \(\mu = 0.6\) (два варианта)?
d) Если направить магнитное поле вертикально вверх в условиях пункта с), какой силы ток надо пустить по проводнику, чтобы проводник начал двигаться (два варианта)?
a) \(F=F_1\cdot\frac{mg-IBL}{mg+IBL}=0.12N\) или \(F=F_1\cdot\frac{mg+IBL}{mg-IBL}=2.08N,\:\) b) \(I=\mu mg/(BL)=20A,\:\) c) \(I=mg(\mu cos\alpha\pm sin\alpha)/(BL)=3A,\:32.8A,\:\) d) \(I=\frac{mg(\mu cos\alpha-sin\alpha)}{BL(cos\alpha+\mu sin\alpha)}=2.65A,\:I=\frac{mg(\mu cos\alpha+sin\alpha)}{BL(cos\alpha-\mu sin\alpha)}=52,4A\)
7. В однородном магнитном поле с индукцией \(B=0.1T\) протон движется по окружности с радиусом \(R=0.1m.\)
a) Чему равна скорость протона, если масса протона равна \(m=1.67\cdot 10^{-27}kg,\) а заряд \(q=1.6\cdot10^{-19}C?\)
b) Включают однородное электрическое поле \(E=100V/m\), вектор напряженности которого параллелен вектору индукции магнитного поля. Через какое время кинетическая энергия протона увеличится в два раза? По какой траектории двигается протон? Сделайте рисунок.
c) Куда надо направить электрическое поле и чему оно должно быть равно, чтобы протон изменил траекторию на прямолинейную?
d) Магнитное поле ограничивают плоскостями, параллельными вектору \(B=0.1T.\) Толщина слоя магнитного поля равна \(h=0.1m.\) Протон влетает в слой перпендикулярно ограничивающим плоскостям. Чему равна скорость протона, если он отклонился на угол \(\alpha=30^0\) после прохождения слоя?
a) \(v=9.6\cdot 10^5m/s,\:\) b) \(t=BR/E=10^{-4}s,\:\) спираль с увеличивающимся шагом, c) \(E=Bv=9.6\cdot10^4V/m,\:\) d) \(v=qBh/(m\cdot sin\alpha)=1.9\cdot10^{6}m/s.\)
8. Дано жесткое проволочное кольцо массы \(m=2gr\), диаметра \(d=8\cdot10^{-2}m,\:\) с сопротивлением \(R=0.04\Omega.\)
a) Полосовой магнит проходит сквозь замкнутое кольцо, сначала быстро, потом медленно. Одинаковый ли заряд переносится индукционным током?
b) Кольцо поместили в однородное магнитное поле \(B=0.5T\), направление которого совпадает c осью кольца. Какой заряд протечет по кольцу при повороте кольца на угол \(\alpha=60^0?\)
c) Какой заряд протечет через кольцо при выключении магнитного поля?
d) Кольцо падает с большой высоты в магнитном поле \(\overrightarrow B,\) которое параллельно вертикальной оси \(z\), направленной вверх, \(B_z(z)=B_{0}+k\cdot z.\). Плоскость кольца сохраняет горизонтальное положение. Найдите установившуюся скорость кольца, если \(k=2.\).
b) \(Q=B\cdot \pi d^2/(8R)=3.14\cdot10^{-2}C,\:\) c) \(Q=B\cdot\pi d^2/(4R)=6.28\cdot 10^{-2}C,\:\) d) \(v=16mgR/(\pi D^2k)^2=8m/s\)
9. Дано жесткое проволочное кольцо диаметра \(d=10^{-1}m.\)
a) К точкам \(A,\;B\) (см. рисунок) подведен ток. Длина дуги \(1\) равна \(\pi d/8.\) Протекающие по кольцу токи создают магнитное поле. Чему равен и куда направлен вектор магнитной индукции в центре кольца?
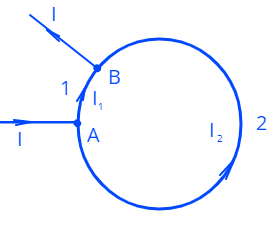
b) Кольцо поместили в вертикальное однородное магнитное поле, направление которого совпадает c осью кольца. Сравните по величине и направлению силы Ампера действующие на проводники \(1\) и \(2.\)
c) Точку \(B\) перенесли, теперь она диаметрально противоположна точке \(A.\) Кольцо подвешено на двух длинных проводах, через которые подводится ток \(I=2A\) в точках \(A\) и \(B\). Плоскость кольца горизонтальна. Индукция вертикального однородного магнитного поля равна \(B=0.1T.\) Кольцо отклонилось от вертикали на угол \(\alpha\) такой, что \(tg\alpha = 1/2.\) Найдите массу кольца.
d) Если в пункте c) изменить условие, и по кольцу будет идти круговой ток, на какой угол отклонится кольцо в этом случае?
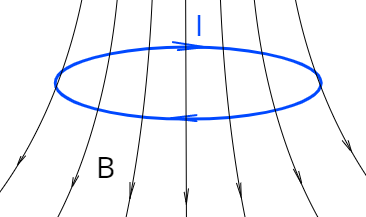
e) Точки \(A\) и \(B\) совместили, по кольцу идет круговой ток \(I=2A.\) Кольцо горизонтально и парит в неоднородном магнитном поле (см. рисунок), вектор индукции которого в точках кольца равен \(B=0.1T\) и составляет угол \(\alpha\) с вертикалью. Найдите угол \(\alpha.\)
a) \(B=0,\:\) b) направления совпадают, \(F_1/F_2=I_1/I_2=7,\:\) c) \(m=4gr,\:\) d) \(0,\:\) e) \(\alpha=39.6^0\)
10. По двум гладким горизонтальным параллельным рельсам, соединенным через сопротивление \(R=20\Omega\), расстояние между которыми равно \(L=0.5m\), может скользить премычка \(MN\), с нулевым сопротивлением и массой \(m=0.1kg\). Система находится в вертикальном магнитном поле \(B,\:|B|=0.4T\). К перемычке приложили постоянную горизонтальную силу \(F=2\cdot 10^{-3}N\) (см. рисунок).
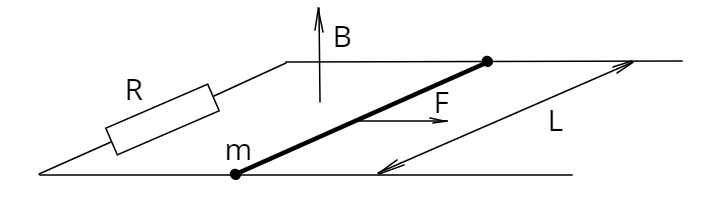
a) Чему равно ускорение перемычки сразу после того, как приложили силу \(F?\)
b) Как будет меняться скорость перемычки? С какой максимальной скоростью может двигаться перемычка ?
c) Чему равна механическая мощность, подводимая к перемычке, и мощность тепловых потерь на сопротивлении при условии, что ее скорость достигла максимального значения?
d) Пусть перемычка двигается с постоянной максимальной скоростью. Силу \(F\) убирают. Какое расстояние пройдет перемычка до остановки?
e) В схему добавили батарею с ЭДС \(\LARGE{\varepsilon}\)\( = 3V\) и внутренним сопротивленим \(r=4\Omega\) (см. рисунок). Чему равен ток и ускорение перемычки сразу после замыкания ключа \(K?\)
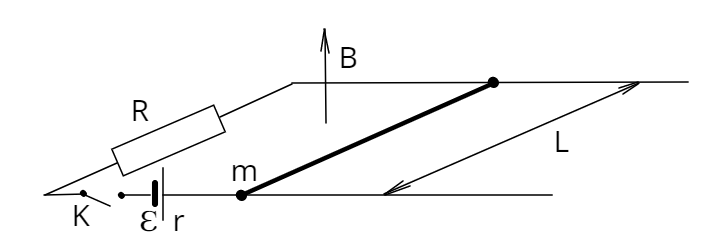
f) Как будет меняться скорость перемычки в этом случае? С какой максимальной скоростью может двигаться перемычка?
g) Когда скорость перемычки стала равна \(v=6m/s,\) к перемычке приложили такую внешнюю силу, что ее скорость перестала изменяться. Чему равна эта сила?
h) Чему равно напряжение на зажимах источника, если скорость перемычки постоянна равна \(v=6m/s?\)
i) Чему равна механическая мощность, подводимая к перемычке, и мощность тепловых потерь на сопротивлении \(R\) при условии, что скорость перемычки постоянна и равна \(v=6m/s?\)
a) \(a=F/m=2\cdot10^{-2}m/s^2,\:\) b) скорость растет \(v_{max}=FR/(BL)^2=1m/s,\:\) c) \(P_F=P_R=F^2R/(BL)^2=2\cdot10^{-3}W,\:\) d) \(s=v_{max}Rm/(BL)^2=50m,\:\)e) \(I=0.125A,\:a=0.25m/s^2,\:\) f) \(v_{max}=\LARGE\varepsilon\\/BL=15m/s,\:\) g) \(F=BL\frac{\LARGE\varepsilon\\-BLv}{R+r}=1.5\cdot10^{-2}N,\:\) h) \(\Delta U=(\LARGE\varepsilon\\R+BLvr)/(R+r)=2.7V,\:\) i) \(P_R=R(\frac{\LARGE\varepsilon\\ - BLv}{R+r})^2=0.1125W,\:P_F=BLv\frac{\LARGE\varepsilon\\ - BLv}{R+r}=0.09W\)
11. Шарик массы \(m\) и с радиусом \(r\) заряжен до потенциала \(U.\)
a) Известно, что в среде без трения шарик может двигаться прямолинейно с постоянной скоростью в скрещенных однородных гравитационном и магнитном полях. Найдите эту скорость \(v_1\), если индукция магнитного поля равна \(B.\)
b) Найдите величину и направление скорости установившегося движения шарика в среде с трением в скрещенных однородных гравитационном и магнитном полях, если известно, что сила трения пропорциональна скорости движения шарика, и скорость его установившегося движения в отсутствии магнитного поля равна \(v_2.\) Движение происходит в плоскости, перпендикулярной вектору индукции магнитного поля.
c) Гравитационное поле в пункте b) заменили на вертикальное электрическое с напряженностью \(E\). Скорость установившегося движения шарика в отсутствии магнитного поля равна \(v_3.\)Чему будет равна скорость установившегося движения шарика в скрещенных электрическом и магнитном полях в среде с трением?
d) Рассмотрим движение шарика в среде без трения в однородных гравитационном и магнитном полях при условии, что магнитное поле с индукцией \(B\) вертикально. Шарик влетает в среду с горизонтальной скоростью \(v_4\). Через какое время \(t_1\) кинетическая энергия шарика удвоится?
e) Через время \(t_1\) после начала движения, когда кинетическая энергия шарика удвоилась, выключают магнитное поле и включают однородное электрическое поле, такое что через время \(t_1/2\) кинетическая энергия шарика становится равной \(0.\) Чему равна напряженность этого электрического поля и под каким углом к горизонту оно направлено? Какой будет траектория движения шарика?
a) \(v_1=mg/(qB),\: q=4\pi \epsilon_0 Ur,\:\) b) \(v^2=v_1^2v_2^2/(v_1^2+v_2^2),\:tg\alpha=v_2/v_1,\:\) где \(\alpha\) - угол между векторами скорости и силы тяжести, c) \(v^2=v_3^2E^2/(E^2+v_3^2B^2),\:\) d) \(t_1=v_4/g,\:\) e) \(E=mg\sqrt{13}, \:tg\alpha = 3/2.\:\)